[Time-series] Stationarity, ARIMA model, Dickey-Fuller test

Time-series 데이터의 Stationarity, AR Model

---

2024.02.12

Stationarity

Weakly Dependent

i.i.d. 가정의 independent 대신에 사용하는 가정. 시차가 커질수록 상관관계가 약해짐을 의미.
\(Corr(X_t,X_{t+h}) \rightarrow 0 \ as \ h \rightarrow \infty\)

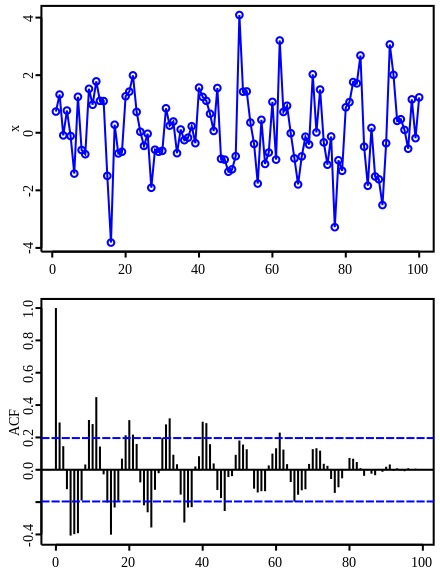
ACF, PACF

Time-series 데이터의 특성을 파악하기 위한 지표.

AutoCovariance Function

시차 $k$ 에 대해 \(X_t, X_{t+k}\) 의 상관관계를 계산한 것.
\(\gamma_k = Cov(X_t, X_{t+k})\) 라 하면
\(\rho_k= Corr(X_t, X_{t+k}) =\) \(\frac{Cov(X_t, X_{t+k})}{\sqrt{Var(X_t)}\sqrt{Var(X_{t+k})}}\) \(= \frac{Cov(X_t, X_{t+k})}{Var(X_t)} = \frac{\gamma_k}{\gamma_0}\)

• 예를 들어 \(AR(1)\) Process의 ACF는 \(\mathcal{\phi}^k\), 즉 계수를 시차 $k$ 만큼 제곱한 수가 나옴.
• 표본에 대해 계산하면 Sample ACF (SACF)
• Time-series 데이터가 독립일 경우 SACF=0, 역은 성립하지 않음

• 아래는 시차에 따른 ACF 값들을 정리한 correlogram

  
  (일단 위키 에서 퍼온 사진)

Partial AutoCovariance Function

Process \(X_t, X_{t+1}, ... , X_{t+k-1}, X_{t+k}\) 에 대해 \(X_t, X_{t+k}\) 의 상관관계를 계산할 때, \(X_{t+1}, ... , X_{t+k-1}\) 의 영향을 제거하고 \(X_t, X_{t+k}\) 이 둘의 관계에만 더 집중한 지표.

• 먼저 두 개의 회귀식을 세운다.
  • \(X_t = \alpha_1 X_{t+1} + \alpha_2 X_{t+2} + ... + \alpha_{k-1} X_{t+k-1} + \epsilon_t\) .
  • \(X_{t+k} = \beta_1 X_{t+1} + \beta_2 X_{t+2} + ... + \beta_{k-1} X_{t+k-1} + \epsilon_{t-k}\) .
• 여기서 \(\epsilon_t = X_t - (\alpha_1 X_{t+1} + \alpha_2 X_{t+2} + ... + \alpha_{k-1} X_{t+k-1})\) 는 \(X_t\) 에서 \(X_{t+1}, ... , X_{t+k-1}\) 의 영향을 모두 제거한 결과이고, 이는 \(\epsilon_{t-k}\) 에 대해서도 마찬가지이다.
• 따라서 그 둘의 상관관계가 어느 정도인지 구한다.
  \(PACF(k) = Corr(\epsilon_t,\epsilon_{t-k})\)
• (PACF를 계산하는 알고리즘에 대한 내용은 생략)

Lag Operator

시점을 뒤로 움직이는 연산자. backshift operator $B$ 라고도 많이 쓰임

\(L(X_t)=X_{t-1}\)
\(L^n(X_t)=L(L^{n-1}(X_t))=X_{t-n}\)

AutoRegressive Process, AR Model

AutoRegressive Process는 특정 시점의 데이터를 이전의 p개 시점의 데이터로 나타낼 수 있는 process를 의미하고, 이를 \(AR(p)\) 모델로 나타낸다.

\(AR(1)\) 이라면 \(X_t=\mathcal{\phi}_1 X_{t-1} + \epsilon_t\)

• \(AR(1)\) Process는 Markov process이기도 하다.
• \(AR(1)\) model is Covariance Stationary iff \(\mathcal{\phi} < 1\)
• \(AR(1)\) 의 예시
  • 이자율(Ornstein–Uhlenbeck process), 이자율 스프레드, real exchange rate(실질 환율), Valuation ratios ¹

\(AR(p)\) process의 평균이 \(\mu\) 이면,
\(X_t - \mu = \mathcal{\phi}_1(X_{t-1} - \mu) + \mathcal{\phi}_2(X_{t-2} - \mu) + \cdots + \mathcal{\phi}_p(X_{t-p} - \mu) + \epsilon_t\)

• 의미에 대해 생각해보면, multiple regression 모델과 다를 게 없다. \(X_t\) 를 이전 p시점까지의 값들로 설명하고자 하는 것이고 \(\mathcal{\phi}_p\) 는 회귀계수, \(\epsilon_t\) 는 white noise이다.

• 위 식에서 우변에 white noise만 남기고 좌변으로 모으면, \((X_t - \mu) - \mathcal{\phi}_1(X_{t-1} - \mu) - \mathcal{\phi}_2(X_{t-2} - \mu) - \cdots - \mathcal{\phi}_p(X_{t-p} - \mu) = \epsilon_t\)

  이 때 Lag operator를 \(LX_t = X_{t-1}\)와 같이 $L$ 을 곱하는 식으로 적용이 가능하다고 하면, 흡사 미분방정식의 \(D=\frac{d}{dx}\)
  \(\mathcal{\phi}(L)(X_t - \mu) = \epsilon_t \ \ where \ \ \mathcal{\phi}(L) = (1 - \mathcal{\phi}_1 L - \mathcal{\phi}_2 L^2 - \cdots - \mathcal{\phi}_p L^p)\)
  이 때 \(\mathcal{\phi}(L)\) 는 AR Operator라고 한다.
  \((1 - \mathcal{\phi}_1 - \mathcal{\phi}_2 - \cdots - \mathcal{\phi}_p)\mu = \delta\) 를 이용하여 \(X_t = \delta + \mathcal{\phi}(L)X_t + \epsilon_t\) 와 같이 쓰기도 한다.

Moving Average Process, MA Model

AR 모델은 특정 시점의 데이터 \(X_t\) 를 과거의 값 \(X_{t-1}, X_{t-2}, ...\) 로 설명하는 모델이고,
MA 모델은 특정 시점의 데이터 \(X_t\) 를 과거의 오차 \(\epsilon_{t-1}, \epsilon_{t-2}, ...\) 로 설명하는 모델이다.
\(MA(q)\) 모델은 다음과 같이 나타낸다.

\[X_t = \mu + \epsilon_t + \theta_1\epsilon_{t-1} + \cdots + \theta_q\epsilon_{t-q}\]

이번에도 Operator를 정의해서 \(\theta(L) = (1 - \theta_1 L - \theta_1 L^2 - \cdots - \theta_p L^q)\) 라 하면

\[X_t = \mu + \theta(L) \epsilon_t\]

이다.

• MA Process는 언제나 Stationary process이다.

ARMA Model

AR모델과 MA모델을 합친 형태.

\[\mathcal{\phi}(L)(X_t - \mu) = \theta(L)\epsilon_t\]

ACF, PACF of AR, MA, ARMA model

\(AR(p)\)

• ACF: 지수적 감소 or 진동
• PACF: $p$ 이후로는 0

\(MA(q)\)

• ACF: $q$ 이후로는 0
• PACF: 지수적 감소 or 진동

\(ARMA(p, q)\)

• ACF: 지수적 감소 or 진동
• PACF: 지수적 감소 or 진동

따라서 Time-series 데이터의 ACF, PACF를 구한 후 어떤 모델을 사용할지 역으로 결정할 수 있다.

Dickey-Fuller test

---

2024.02.12

Stationarity에 대한 테스트로, trend가 있는지를 테스트하는 것. t-Test 를 기반으로 한다.

• \(AR(1)\) 모델 \(X_t = \mathcal{\phi}X_{t-1}+\epsilon_t\) 을 예로 들고,
• 가설을 세운다.
  \(H_0: \mathcal{\phi}=1\) (unit root, non-stationary)
  \(H_1: \lvert \mathcal{\phi} \rvert < 1\) (stationary)
• OLS로 \(AR(1)\) 모델을 fit시킨 후, 다음과 같이 t-statistic을 계산하고 테스트를 진행한다.
  \(t_{\mathcal{\phi}=1} = \frac{\hat{\mathcal{\phi}}-1}{s.e.(\hat{\mathcal{\phi}})}\)
  보통 회귀에 대해 배울 때 \(\beta\) 라고 쓰던 변수가 \(\mathcal{\phi}\) 로 바뀐 것이라고 생각하면 되겠다.

코드

(추후 추가…)

Difference(차분)

---

2024.02.12

trend를 제거하기 위해 사용하는 방법으로, 데이터 자체가 아닌 변화폭을 기준으로 보는 것

1차 차분: \(Z_t = X_t - X_{t-1}\)
2차 차분: \(Z_t = (X_t - X_{t-1}) - (X_{t-1} - X_{t-2}) = X_t - 2 X_t{t-1} + X_{t-2}\)

ARIMA Model

AutoRegressive Integrated Moving Average \(ARIMA(p,d,q)\) 는 \(ARMA(p,q)\) 에 $d$ 차 차분 이 추가된 것.

References

---

https://datalabbit.tistory.com/117
https://direction-f.tistory.com/65
https://www.stat.unm.edu/~ghuerta/tseries/week6_1.pdf

1. https://ocw.mit.edu/courses/18-s096-topics-in-mathematics-with-applications-in-finance-fall-2013/resources/mit18_s096f13_lecnote8/ ↩