KL Divergence

2024.05.18

---

Information Entropy

\(I(x) = -log(p(x))\)
\(H(x) = \sum -log(p(x)) \ p(x)\) (Cross Entropy)

어떤 사건을 불확실성의 정도를 표현하기 위해 발생할 확률이 1이면 0, 발생할 확률이 0에 가까워질수록 큰 수를 맵핑할 수 있도록 로그함수를 사용해 나타낸다.

KL Divergence

\[\begin{aligned} D_{KL}(P \vert \vert Q) & = \int _{-\infty} ^{\infty} P(x)log\Big(\frac{P(x)}{Q(x)}\Big) dx = \mathbb{E}_{X \sim P(x)}\Biggr[ log\frac{P(x)}{Q(x)} \Biggr] \\ & = \int _{-\infty} ^{\infty} -log\Big(\frac{Q(x)}{P(x)}\Big) P(x) dx \end{aligned}\]

• KL Divergence는 두 분포가 얼마나 유사한지 비교하기 위해 정의되는 값으로, \(I(x) = -log(p(x))\) 에서 \(p(x)\) 대신 \(\frac{Q(x)}{P(x)}\) 를 넣은 것과 같은 형태이다. 어떤 분포와 다른 분포를 비교할 수 있는 값에 대해 기댓값을 구하기 위하여, \(P(x)\)와 비교한 \(Q(x)\)의 상대적인 값에 대해 기댓값을 구하는 것이다.
  • (아마 그래서?) relative entropy 라고도 불린다. ¹
• non-negative의 값이 나오고, 0이면 두 분포가 완전히 동일한 경우. (\(log(\frac{P(x)}{Q(x)})\)의 값이 항상 1이므로 log 값은 0이니까)

Examples

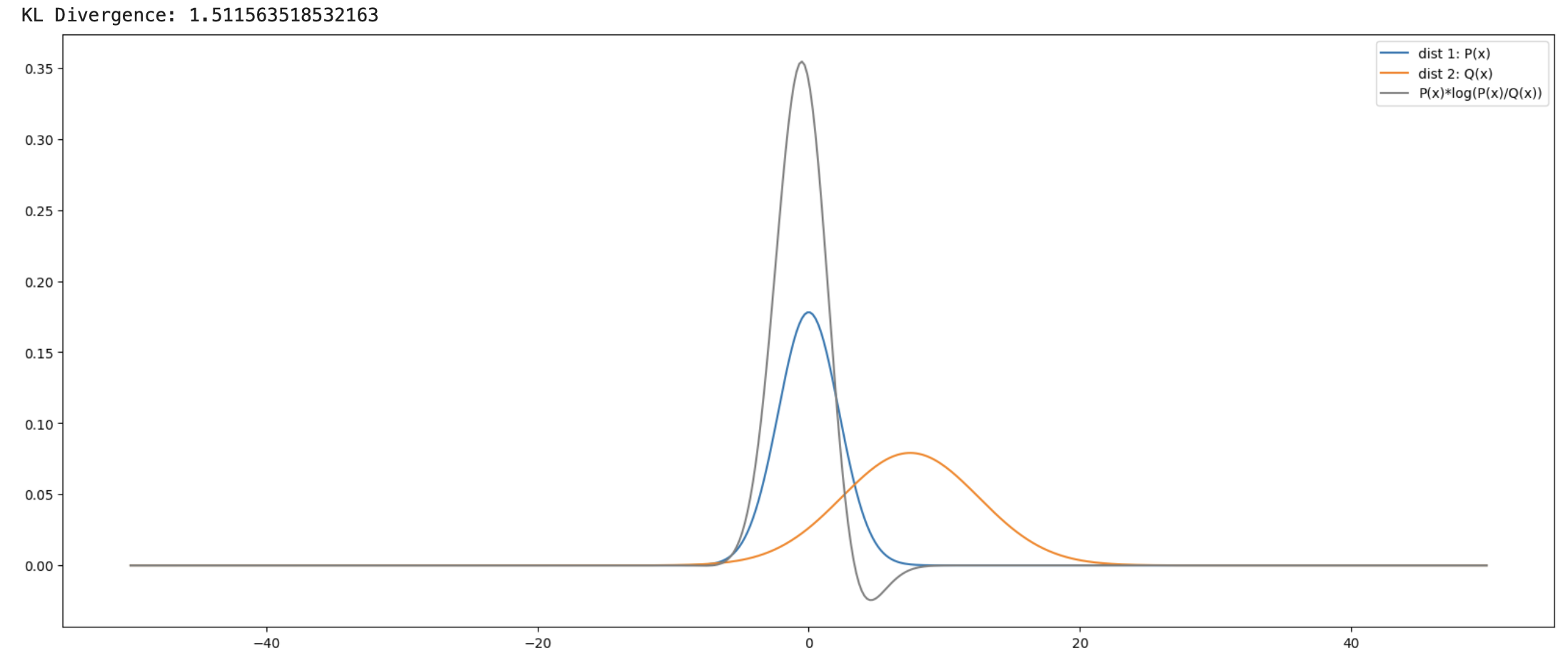
파란색: \(P(x)\)
주황색: \(Q(x)\)
회색: \(P(x) \frac{P(x)}{Q(x)}\)

두 분포는 모두 정규분포로 테스트했다.

\[P(x): \mu=0, \sigma=2.2395 \quad Q(x): \mu=7.484, \sigma=5.0429\]

이 두 정규분포에 대한 KL Divergence는 1.512

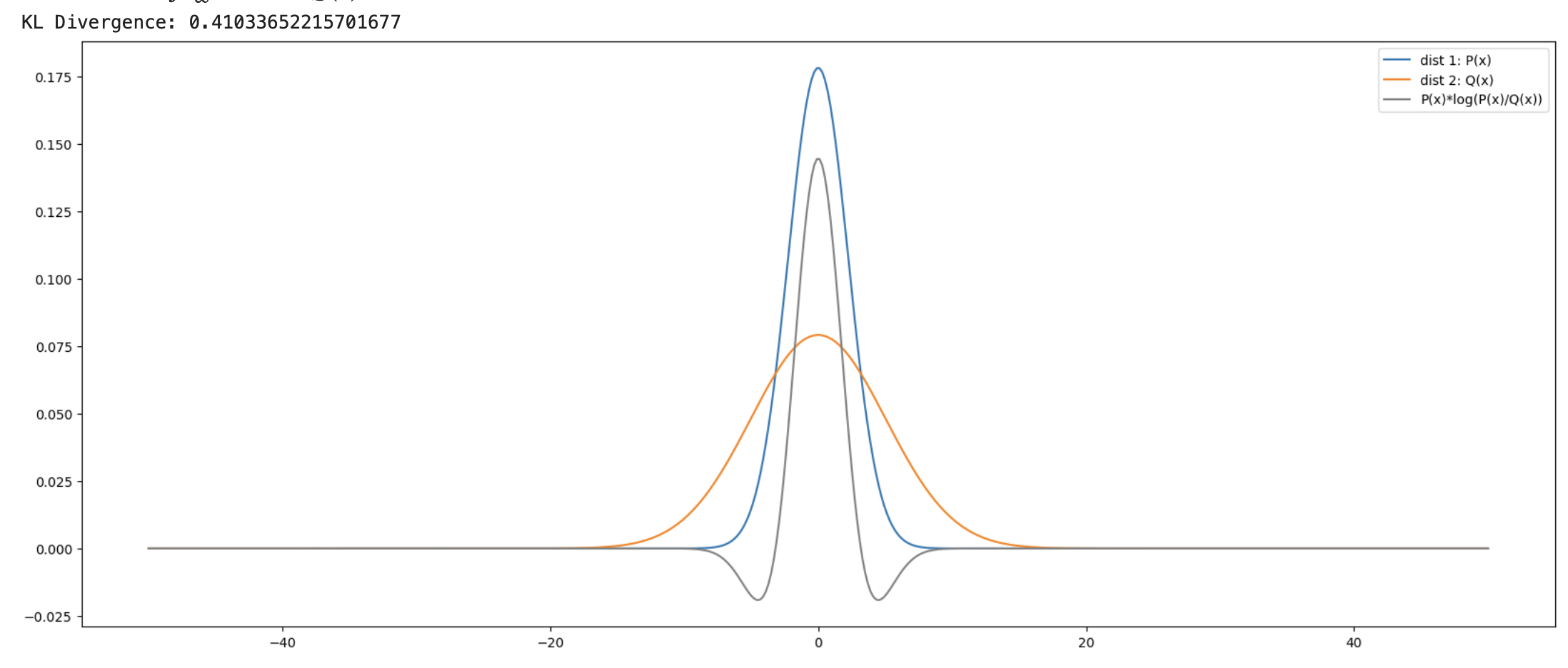
테스트1: 표준편차가 다른 두 분포의 평균을 똑같이 0으로 맞춤

\[P(x): \mu=0, \sigma=2.2395 \quad Q(x): \mu=0, \sigma=5.0429\]

두 정규분포에 대한 KL Divergence는 0.41

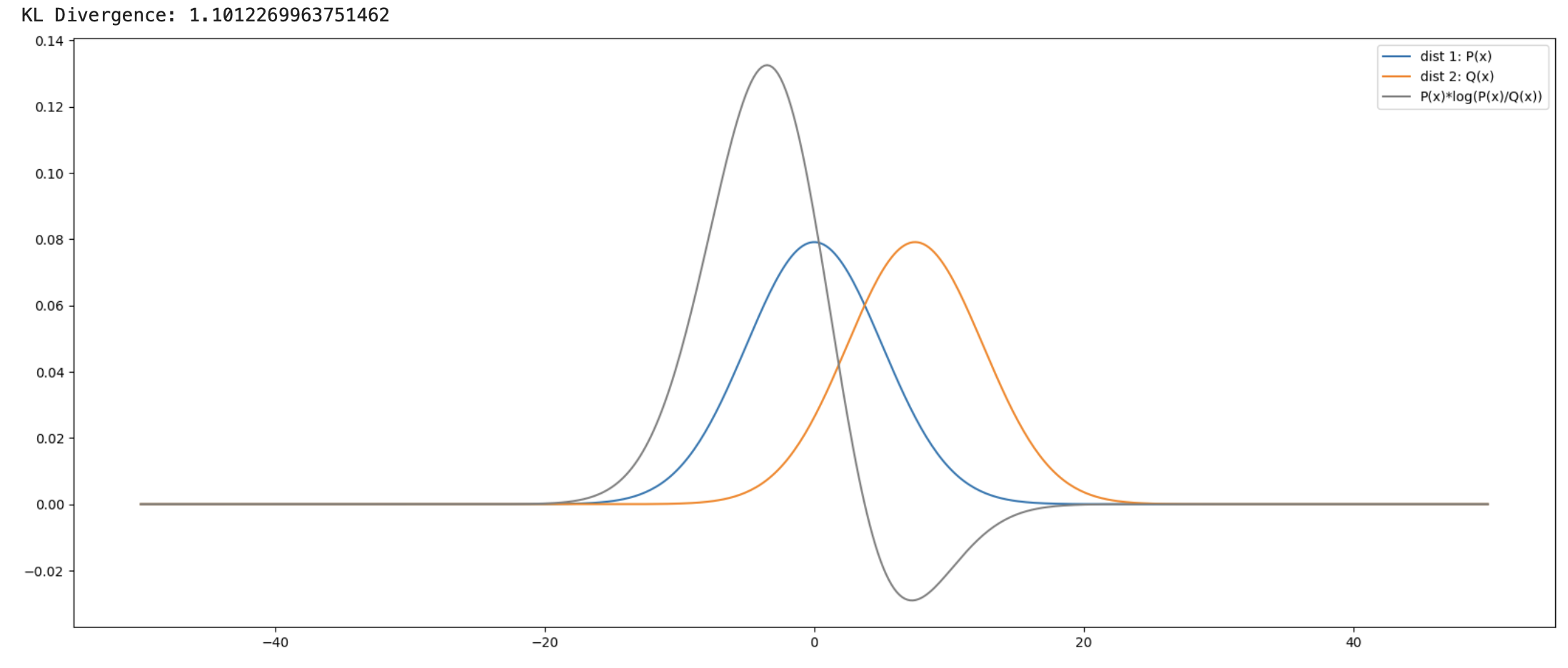
테스트2: 평균이 다른 두 분포의 표준편차를 똑같이 맞춤

\[P(x): \mu=0, \sigma=5.0429 \quad Q(x): \mu=7.484, \sigma=5.0429\]

두 정규분포에 대한 KL Divergence는 1.101

결국… 어느 경우에서 KL Divergence가 더 작을지는 그냥 계산해봐야 알 수 있다.

2024.05.18

References

---

1. https://en.wikipedia.org/wiki/Kullback–Leibler_divergence ↩