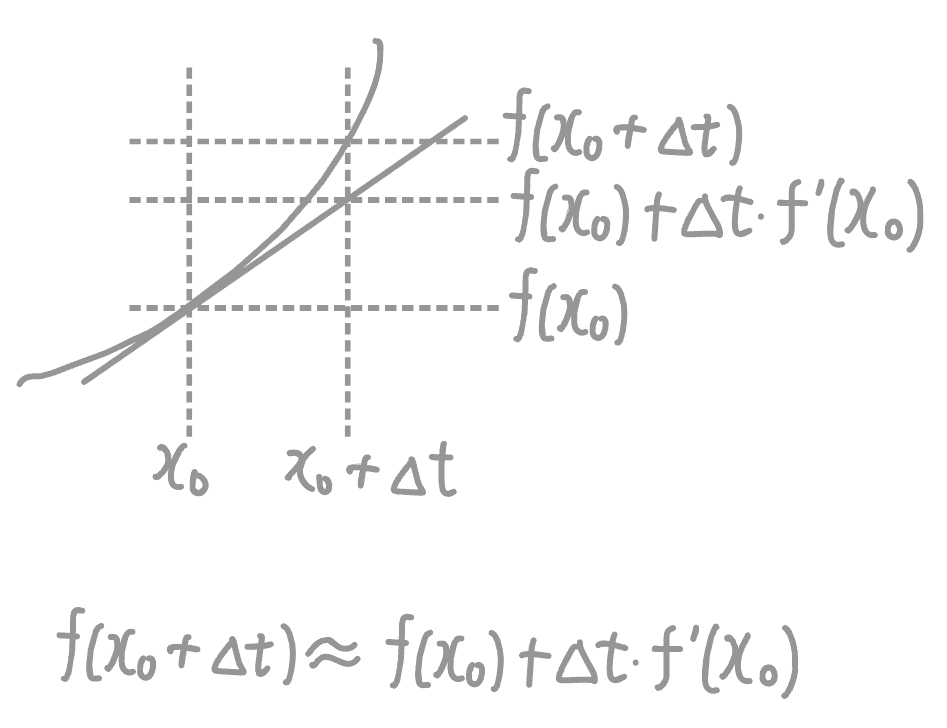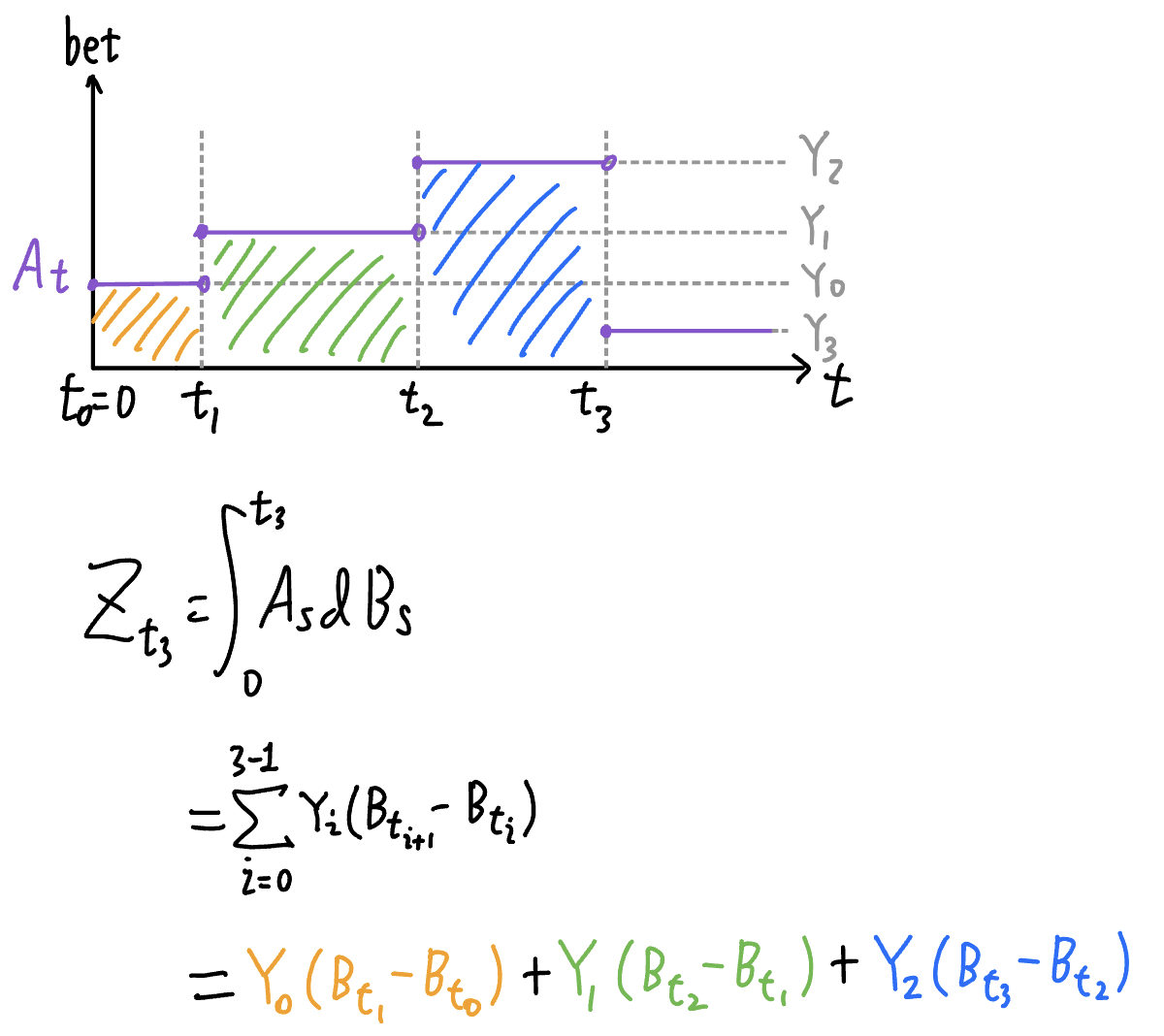3. Stochastic Integration
https://www.math.uchicago.edu/~lawler/inprogress
3.1 What is stochastic calculus?
2024.02.06
- Calculus의 핵심 아이디어는 어떤 함수의 rate of change를 통해 그 함수를 알아낼 수 있다는 것. \(\frac{df}{dt} = f'(t) = C(t, f(t)), f(t) = x_0 + \int_{0}^{t}{C(s, f(s))}ds\)
- Euler’s method에 따라 \(f((k+1)\Delta t) = f(k\Delta t) + \Delta t \ C(k\Delta t, f(k \Delta t))\) 와 같이 쓸 수 있다.
미분적분학I에서 보는 그 내용
![euler's method]()
- Stochastic calculus도 이와 비슷하나, 여기에는 ‘변화’에 randomness가 추가된다.
앞으로 아래와 같은 SDE(Stochastic Differential Equation)가 어떻게 make sense하게 될 수 있는지 알아볼 것.
\(dX_t = m(t, X_t) + \sigma(t, X_t) dB_t\) \(\cdots\) (3.1) where \(B_t\) is a standard Brownian motion- 위 식의 의미는, $t$ 시점에서 \(X_t\) 가 drift는 $m$이고 variance는 \(\sigma\) 인 Brownian motion처럼 변화한다는 것
- 일반적인 calculus보다 풀기 어렵고 보통은 numerical한 방법이 필요하다. 그중 하나는 Monte Carlo를 활용한 stochastic Euler method: \(X((k+1)\Delta t) = X(k\Delta t) + \Delta t \ m(k\Delta t, X(k \Delta t)) + \sqrt{\Delta t} \ \sigma(k\Delta t, X(k \Delta t)) N_k\)
where \(N_k \sim N(0,1)\)
- Stochastic calculus에서는 \(X_t = X_0 + \int_{0}^{t}{m(s,X_S)ds} + \int_{0}^{t}{\sigma(s,X_S)dB_s}\) 를 만족하는 \(X_t\) 를 위 (3.1)과 같은 SDE의 해라고 본다.
- 이중 \(ds\) term은 일반적인 calculus와 다를 게 없고, 그 뒤의 term 즉 \(\int_{0}^{t}{A_s dB_s}\) 의 정확한 의미가 무엇인지가 주요한 문제이다.
- 이를 다루는 여러 방법들이 있지만, 여기서는 mathematical finance에서 가장 흔히 사용되는 Itô integral에 대해 알아본다.
3.2 Stochastic integral
2024.02.06
- \(B_t\) 가 1차원의 standard Brownian motoin (drift가 0, variance가 1) w.r.t. the \(\mathcal{F}_n\) 라고 할 때, 다음과 같은 (stochastic) process를 정의하고자 한다.
\(Z_t = \int_0^tA_sdB_s\) - discrete stochastic integral에서처럼 \(A_s\) 는 베팅 금액으로 생각할 수 있음 음수일 때는 흡사 숏
3.2.1. Review of Riemann integration
적분 구간을 여러 partition으로 나누고 step function으로 근사한 뒤 극한을 취한다는 기본적인 내용
3.2.2. Integration of simple process
simple process는 마치 리만 적분에 사용되는 step function과 같은 것
- 이는 베팅을 하는 시점들이 유한(finite)하다고 생각하면 되고, \(Z_t=\int_0^t{A_sdB_s}\) 를 다음과 같이 정의할 수 있다. \(Z_{t_j}=\sum_{i=0}^{j-1}{Y_i[B_{t_{i+1}}-B_{t_i}]} \quad (A_t=Y_j)\)
![integrating simple process]()
\(t_j \ne j\) 인지 아닌지 빨리 이해가 안돼서 이해하는 데에 오래 걸린 부분
저렇게 보는 것 자체가 르베그 적분 느낌이 난다.
Proposition 3.2.1.
Properties of stochastic integral of simple process
- Linearity
- Martingale property
- Variance rule
- Continuity : Random Walk의 적분과 비교했을 때, Simple process의 적분은 연속성이 있다. Brownian Motion이 연속적이기 때문
3.2.3. Integration of continuous process
- 이번에는 \(A_t\) 가 continuous path를 가지는 process를 적분
- 다음의 Lemma를 이용
Lemma 3.2.2.
continuous path를 가지는 process \(A_t\) 와 \(\forall t \lvert A_t \rvert \le C\) 인 \(C < \infty\) 가 있을 때, 모든 $t$ 에 대해 다음을 만족하는 simple process \(A_t^{(n)}\) 들이 존재한다.
\[\lim_{n \rightarrow \infty} \int_{0}^{t}{\mathbb{E}[\lvert A_s - A_s^{(n)} \rvert^2]ds}=0 \quad where \ \forall n,t, \ A_t^{(n)} \le C\]- 위 Lemma를 이용해 bounded, continuous process \(A_s\) 의 적분을 다음과 같이 같이 정의할 수 있다.
\(Z_t = \int_{0}^{t}{A_sdB_s} = \lim_{n \rightarrow \infty} \int_{0}^{t}{A_s^{(n)}dB_s}\)
continuous path는 step function처럼 생긴 것들을 더 촘촘하게 만들어서 정의. 흡사 리만적분
Proposition 3.2.3.
Continuous path를 가지는 process의 적분이 가지는 4개의 property들은 위 Proposition 3.2.1. 과 같다.
Proposition 3.2.5.
반드시 bounded가 아니어도 정의가 가능하나, 경우에 따라 위 4개의 property들 중 martingale property가 성립하지 않을 수 있다. (Section 4.1 참고)
- 이제 \(X_t = X_0 + \int_{0}^{t}{A_sdB_s}\) 을 만족하는 \(X_t\) 는 \(dX_t = A_tdB_T\) 와 같이 stochastic differential의 형태로 써낼 수 있고, 지금까지 continuous process \(A_t\) 에 대해 이를 정의했다. 또한 \(X_t\)는 $t$ 에 대한 연속 함수이다.
- bounded continuous function \(\mathbb{\phi}\) 에 대해 \(dX_t = \mathbb{\phi}(X_t)dB_t\) 를 풀어내는 것은 더 어려우나(Section 3.5 마지막 부분 참고), 이를 Euler rule로 시뮬레이션하는 것은 다음과 같이 straightforward하다. (95p) \(X_{t+\Delta t} = X_t +\mathbb{\phi}(X_t)\sqrt{\Delta t} \ N\) where \(N_k \sim N(0,1)\)
- usual calculus의 rule을 stochastic calculus에 동일하게 적용할 수 없다. 예를 들어 \(\int_{0}^{t}{B_sdB_s}=\frac{1}{2}[B_t^2-t]\ne\frac{B_t^2}{2}\) 이다.
- 이런 차이를 위해 사용하는 것이 다음 section에서 나오는 Itô’s lemma이다.
- \(\int_{0}^{t}{B_sdB_s}\ne\frac{B_t^2}{2}\) 이라는 것에 대해서는, expectation을 구해보면 \(\mathbb{E}[\frac{B_t^2}{2}]=\frac{t}{2}\ne 0\) 임을 알 수 있다. (96p)
- 위 예시의 \(\frac{1}{2}[B_t^2-t]\) 처럼 non-normal distribution이 나올 수도 있다.
Theorem 3.2.6.
\(A_t\) 가 continuous or piecewise continuous path를 가지는 adapted process이고 \(Z_t=\int_{0}^{t}{A_sdB_s}\) 이면 \(\langle Z \rangle _t=\int_{0}^{t}{A_s^2ds}\)
여기서 \(A_s=\sigma\) 로 상수이면 quadratic variation은 익숙한 값인 \(\sigma^2t\) 가 나온다.
Quadratic variation은 \(\mathbb{E}[\langle Z \rangle _t] = \mathbb{E}\biggr[ \int_{0}^{t}{A_s^2ds} \biggr] = \int_{0}^{t}{\mathbb{E}[A_s^2]ds}\) 을 mean으로 가지는 r.v.이다.
3.3 Itô’s formula
2024.02.07
Theorem 3.3.1.
\(f \in C^2\) 와 standard brownian motion \(B_t\), 그리고 모든 $t$ 에 대해
\(df(B_t) = f'(B_t)dB_t + \frac{1}{2} f''(B_t)dt\)
이건 Theorem 3.4.1.까지 본 후에 다시
3.4 More versions of Itô’s formula
2024.02.07
Theorem 3.4.1.
\(f(t,x)\) 가 $t$ 에 대해서는 \(C^1\), $x$ 에 대해서는 \(C^2\) 이고, \(B_t\) 는 standard brownian motion일 때, \(df(t, B_t) = \partial _x f(t, B_t)dB_t + \biggr[\partial _t f(t, B_t) + \frac{1}{2} \partial _{xx} f(t,B_t) \biggr] dt\)
Section 3.3과 3.4의 Itô’s Lemma는 책 외에 찾아봤던 내용들을 종합해서 정리했다.
Itô’s lemma는 taylor expansion으로부터 유도해낼 수 있다. 다만 이는 엄밀한 증명은 아닌 heuristic한 방법이다. 1
- 먼저 미분적분학1에서 배우는 taylor expansion의 형태는 \(f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \cdots\) 이다.
이변수 함수 \(f(t,x)\) 에 대한 taylor expansion은
\[\begin{aligned} \small f(t, x) & = f(t_0, x_0) + \frac{\partial f(t_0,x_0)}{\partial t}(t - t_0) + \frac{\partial f(t_0,x_0)}{\partial x}(x - x_0) \\ & + \frac{1}{2!}\biggr[ \frac{\partial ^2 f(t_0,x_0)}{\partial t^2}(t - t_0)^2 + 2 \frac{\partial ^2 f(t_0,x_0)}{\partial t \partial x}(t - t_0)(x - x_0) + \frac{\partial ^2 f(t_0,x_0)}{\partial x^2}(x - x_0)^2 \biggr] \\ & + \frac{1}{3!}\biggr[ \frac{\partial ^3 f(t_0,x_0)}{\partial t^3}(t - t_0)^3 + 3 \frac{\partial ^3 f(t_0,x_0)}{\partial t^2 \partial x}(t - t_0)^2(x - x_0) \\ & + 3 \frac{\partial ^3 f(t_0,x_0)}{\partial t \partial x^2}(t - t_0)(x - x_0)^2 + \frac{\partial ^3 f(t_0,x_0)}{\partial x^3}(x - x_0)^3 \biggr] \\ & + \cdots \end{aligned}\]이고2, 이와 유사하게 다음과 같은 수식도 존재한다.
\(f(t + dt, x + dx) - f(t, x) = \frac{\partial f}{\partial t}dt + \frac{\partial f}{\partial x}dx + \frac{1}{2!}\biggr[ \frac{\partial ^2 f}{\partial t^2}dt^2 + 2 \frac{\partial ^2 f}{\partial t \partial x}dtdx + \frac{\partial ^2 f}{\partial x^2}dx^2 \biggr] + \cdots\)
여기서 좌변은 \(df\) 라 하자.Itô process \(X_t\) 가 \(dX_t = \mu_t dt + \sigma_t dB_t\) 일 때, 위 식의 $x$ 를 \(X_t\) 로 대체하기 위해 \(dx\) 에 \(\mu_t dt + \sigma_t dB_t\) 를 대입하면
\(df = \frac{\partial f}{\partial t}dt + \frac{\partial f}{\partial x}(\mu_t dt + \sigma_t dB_t) + \frac{1}{2!}\biggr[ \frac{\partial ^2 f}{\partial t^2}dt^2 + 2 \frac{\partial ^2 f}{\partial t \partial x}dt(\mu_t dt + \sigma_t dB_t) + \frac{\partial ^2 f}{\partial x^2}(\mu_t dt + \sigma_t dB_t)^2 \biggr] + \cdots\)\(dt \rightarrow 0\) 일 때, \(dt^2\) 와 \(dtdB_t\) 는 \(dB_t^2\) 보다 빠르게 0에 근접한다. (\(dB_t^2\) 는 \(O(dt)\) 이므로)
\[\begin{aligned} df & = \frac{\partial f}{\partial t}dt + \frac{\partial f}{\partial x}(\mu_t dt + \sigma_t dB_t) + \frac{1}{2!}\biggr[\frac{\partial ^2 f}{\partial x^2}\sigma_t^2 dt \biggr] \\ & = \biggr[ \frac{\partial f}{\partial t} + \frac{\partial f}{\partial x}\mu_t + \frac{\sigma_t^2}{2}\frac{\partial ^2 f}{\partial x^2} \biggr] dt + \sigma_t \frac{\partial f}{\partial x} dB_t \\ \end{aligned}\]
\(dt^2=0\), \(dtdB_t=0\) 이라 두면3, \(dt, dB_t, dB_t^2\) term들만 남을 수 있으므로 위의 expansion에서 대부분의 항들은 사라진다. 4- Theorem 3.3.1.의 경우처럼 \(X_t\) 가 \(\mu_t=0, \sigma_t=1\) 로 standard brownian motion인 경우에는 다음과 같이 더 간단해진다.
위 Itô’s lemma에서 \(\mu\) 와 $t$ 로 미분한 부분을 제거하면
\(df(t, X_t) = \frac{1}{2}\frac{\partial ^2 f}{\partial x^2} dt + \frac{\partial f}{\partial x} dB_t\)
\(df(B_t) = f'(B_t)dB_t + \frac{1}{2} f''(B_t)dt\) 와 같은 형태
Definition (GBM)
SDE가 다음과 같은 형태로 나타날 경우 process \(X_t\) 는 Geometric Brownian Motion이다.
\(dX_t = X_t(m dt + \sigma dB_t)\)
위 SDE의 해를 구하면5
- 일단 \(\frac{dX_t}{X_t}=m dt + \sigma dB_t\) 이고, \(\frac{d(lnX_t)}{dX_t}=\frac{1}{X_t}\) , \(d(lnX_t)=\frac{dX_t}{X_t}\) 이므로 \(d(lnX_t) = m dt + \sigma dB_t\) 와 같이 정리
- Theorem 3.3.1. 에 따라 \(df(t, X_t) = \frac{1}{2}\frac{\partial ^2 f}{\partial x^2} dt + \frac{\partial f}{\partial x} dB_t\) 이고 \(f(t, X_t) = ln(X_t)\) 라 하면
\(X_t\) 가 standard BM \(d(lnX_t) = (lnX_t)' dX_t + \frac{1}{2}(lnX_t)'' (dX_t)^2\) - 계산하면 \(d(lnX_t) = \frac{1}{X_t} dX_t - \frac{1}{2}\frac{1}{X_t^2} (dX_t)^2\)
- 그리고 \((dX_t)^2\) 는 위 SDE의 quadratic variation으로 계산해서 대입하면 \((dX_t)^2 = (m X_t dt + \sigma X_t dB_t)^2 = m^2X_t^2(dt)^2 + m \sigma X_t^2 dt dB_t + \sigma^2X_t^2(dB_t)^2\) 이 때 \(dt \rightarrow 0\) 이면 \((dX_t)^2 = \sigma^2X_t^2dt\) 가 된다. \(dt=dB_t^2\)
- \((dX_t^)2 = \sigma^2X_t^2dt\) 를 대입하면
\(d(lnX_t) = \frac{1}{X_t} dX_t - \frac{1}{2}\frac{1}{X_t^2} \sigma^2X_t^2dt = \frac{dX_t}{X_t}-\frac{1}{2}\sigma^2dt\) 이고 여기서 \(\frac{dX_t}{X_t}\) 를 \(m dt + \sigma dB_t\) 로 바꾸면 와 \(d(lnX_t) = m dt + \sigma dB_t - \frac{1}{2}\sigma^2dt\) 이제 적분
\[\begin{aligned} \int_{0}^{t}{d(lnX_t)} & = \int_{0}^{t}{m dt} + \int_{0}^{t}{\sigma dB_t} - \int_{0}^{t}{\frac{1}{2}\sigma^2dt} \\ ln(X_t) & = mt + \sigma B_t - \frac{1}{2}\sigma^2 t + C \\ ln(X_t) - ln(X_0) & = mt + \sigma B_t - \frac{1}{2}\sigma^2 t \\ ln(\frac{X_t}{X_0})& = mt + \sigma B_t - \frac{1}{2}\sigma^2 t \\ \frac{X_t}{X_0}& = e^{mt + \sigma B_t - \frac{1}{2}\sigma^2 t} \\ X_t& = X_0 e^{(m - \frac{1}{2}\sigma^2)t + \sigma B_t} \\ \end{aligned}\]또는 \(X_t = X_0 exp((m - \frac{1}{2}\sigma^2)t + \sigma B_t)\)
처음에 잘못 푼 과정
$$ \begin{aligned} dX_t & = X_t(m dt + \sigma dB_t) \\ \int_{0}^{t}{\frac{dX_t}{X_t}} & = \int_{0}^{t}{m dt} + \int_{0}^{t}{\sigma dB_t} \\ ln(X_t) & = mt + \sigma B_t + C \\ X_t & = e^{mt + \sigma B_t + C} \\ & = X_0e^{mt + \sigma B_t} = X_0 exp(mt + \sigma B_t)\\ \end{aligned} $$Example 3.4.1.
3.5 Diffusions
2024.02.08
- 함수 \(m(t,x), \sigma(t,x)\) 에 대해 \(X_t\) 가 다음과 같은 형태의 SDE를 만족하면 \(X_t\) 를 Diffusion process라 한다. (111p)
\(dX_t = m(t,X_t)dt + \sigma(t,X_t)dB_t\) - 아래와 같이 coefficient term들이 t와 무관하면 time-homogenous라고 한다.
\(dX_t = m(X_t)dt + \sigma(X_t)dB_t\) - Diffusion process는 Markov process이다.
- diffusion의 시뮬레이션은 아래와 같은 stochastic Euler rule로 가능 \(X_{t+\Delta t} = X_t + m(t, X_t)\Delta t + \sigma(t, X_t) \sqrt{\Delta t} N\) where \(N \sim N(0,1)\)
- Generator of diffusion (wikipedia)
\(Lf(x) = \lim_{t \downarrow 0} \frac{\mathbb{E}^x[f(X_t)]-f(x)}{t}\)
3.6 Covariation and the product rule
2024.02.08
- standard BM \(B_t\) 에 대해 \(dX_t = H_tdt+A_tdB_t, \ dY_t = K_tdt+C_tdB_t\) 라 하자.
- Covariation \(\langle X,Y \rangle _t = \int_{0}^{t}{A_sC_sds}\) 또는 \(d\langle X,Y \rangle _t = A_tC_tdt\)
Theorem 3.6.1. stocastic product rule
\[d(X_tY_y) = X_t dY_t + Y_t dX_t + d\langle X,Y \rangle _t\]또는
\[\begin{aligned} X_tY_t & = X_0Y_0 + \int_{0}^{t}{X_sdY_s} + \int_{0}{t}{Y_sdX_s} + \int_{0}{t}{\langle X,Y \rangle _s} \\ & = X_0Y_0 + \biggr[ \int_{0}^{t}{X_sK_sds} + \int_{0}^{t}{[X_sC_s]dB_S} \biggr] \\ & + \biggr[ \int_{0}^{t}{Y_sH_sds} + \int_{0}^{t}{[Y_sA_s]dB_S} \biggr] \\ & + \int_{0}^{t}{A_sC_sds} \\ & = X_0Y_0 + \int_{0}^{t}{[X_sK_s+Y_sH_s +A_sC_s]ds} + \int_{0}^{t}{[X_sC_s+Y_sA_S]dB_S} \\ \end{aligned}\]3.7 Several Brownian motions
2024.02.08
지금까지의 적분들은 모두 w.r.t. single BM 이었음
- independent BMs w.r.t. \(\mathcal{F_t}\) \(B_t^1, ... ,B_t^d\) 와 adapted process \(A_t^1, ... ,A_t^d\) 대해, 여러 개의 BM에 대한 SDE의 형태는
\(dX_t = H_tdt + \sum_{j=1}^{d}{A_t^jdB_t^j}\) - \(\langle B^i, B^j \rangle = 0, \ i \ne j\) 이다.
- \(d\langle X,Y \rangle _t = \sum_{j=1}^{d}{A_t^jC_t^jdt}\) .
- 그리고 Itô’s formula 역시 더 일반적으로 정의할 수 있다. (Theorem 3.7.1., 3.7.2.)
Theorem 3.7.2.
공간의 standard BM \(B_t = (B_t^1, . . . , B_t^d) in \mathbb{R}^d\) 에 대해 함수 \(f:[0,\infty) \times \mathbb{R}^d\) 가 $t$ 에 대해 \(C^1\) , \(\textbf{x} \ in \ \mathbb{R}^d\) 에 대해 \(C^2\) 일 때
\(df(t,B_t) = \nabla f(t,B_t) \cdot dB_t+ \biggr[ \dot{f}(t,B_t)+\frac{1}{2}\nabla^2 f(t,Bt)\biggr ]dt\)
* \(\nabla f(t,B_t) \cdot dB_t\) 는 벡터들의 내적
** Theorem 3.4.1. 에서 본 Itô’s lemma 형태는:
\(df = \biggr[ \frac{\partial f}{\partial t} + \frac{\partial f}{\partial x}\mu_t + \frac{\sigma_t^2}{2}\frac{\partial ^2 f}{\partial x^2} \biggr] dt + \sigma_t \frac{\partial f}{\partial x} dB_t\)
여기서 공간에 대해 미분하는 항들만 여러 공간에 대한 형태로 바뀐 것
3.8 Exercises
(Skip)