측도론으로 정의하는 확률

측도론으로 정의하는 확률

---

고등학교에서 배운 확률의 정의와 한계

확률과 통계 (천재교육/이준열, 2015 교육과정) 47p

핵심은 특정 사건의 개수를 사건의 개수/개수로 정의했다는 점. 따라서 표본 공간의 크기가 무한히 큰 경우 등 개수로 정의하지 못하는 경우에 대해서는 이러한 정의로 다룰 수 없게 된다.
처음에는 확률에 대한 더 엄밀한 정의가 왜 필요한지 이해하는 것도 오래 걸렸다.

Probability Space (확률 공간)

Measure Space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$의 measure $\mathbb{P}$가 확률일 경우 이를 Probability Space라고 한다.

• measure $\mathbb{P}$는 위의 ‘수학적 확률’의 의미를 가져온 것이고, 이 $\mathbb{P}$가 만족해야 할 세 가지 공리를 Kolmogorov Axiom이라 한다.

  1. $\mathbb{P}(E)\in \mathbb{N},\mathbb{P}\ge 0\mathrm{\forall }E\in \mathcal{F}$  
  2. $\mathbb{P}(\mathrm{\Omega })=1$  
  3. $\mathbb{P}(\bigcup _{n=1}^{\mathrm{\infty }}{A}_n)=\sum _{n=1}^{\mathrm{\infty }}\mathbb{P}(A_n)$  

  일반적인 measure의 조건과 달리 $\mathbb{P}(\mathrm{\Omega })=1$ 이다.

• Measure Space와 sigma algebra의 개념을 도입하면, 기존에 확률공간의 사건이라고 부르던 것들은 $\mathcal{F}$의 원소가 된다. 사건을 단지 집합의 원소로 봄으로써 엄밀함을 제고하게 된다.

Random Variable (확률변수)

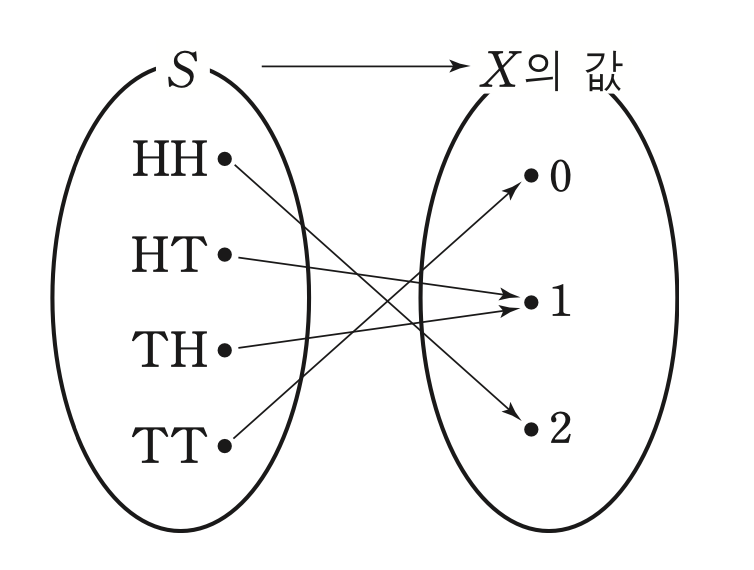
확률과 통계 (천재교육/이준열, 2015 교육과정) 84p

Probability Space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ 에 대해 다음을 만족하는 함수 $X:\mathrm{\Omega }\to \mathbb{R}$ 를 Random Variable이라 한다.

$$w\in \mathrm{\Omega };X(w)\in B\in \mathcal{F}\mathrm{\forall }BorelsubsetBof\mathbb{R}$$

• 확률변수는 sigma algebra의 원소를 실수값으로 매핑하는 함수이다.
• B의 preimage(역상)가 sigma algebra에 존재해야 확률변수가 정의될 수 있다.

Distribution (확률분포)

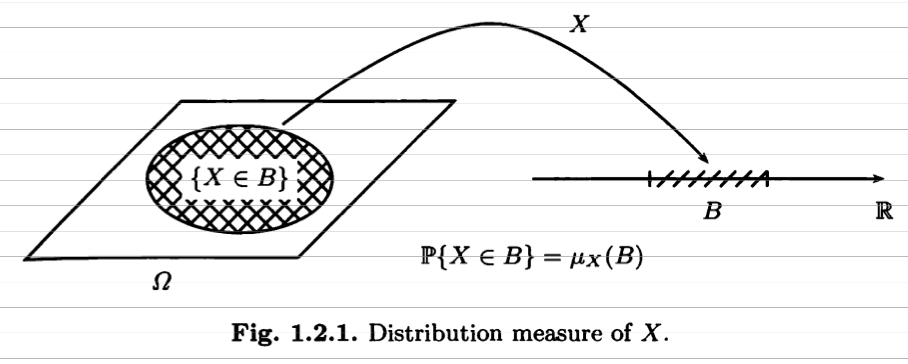
Shreve, S. E. (2010). Stochastic calculus for finance II: Continuous-time models. Springer. p.9

Probability Space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ 에 대한 Random Variable $X$가 있을 때, $X$에 대한 distribution ${\mu }_X$는 mass를 $B$로 assign하는 measure이다. 이 때 ${\mu }_X(B)=\mathbb{P}(X\in B)$ 이다.
B는 $\mathbb{R}$에 대한 Borel subset

• 확률분포는 measure의 일종.

Expectation (기댓값)

2024.01.31

References

---

Shreve, S. E. (2010). Stochastic calculus for finance II: Continuous-time models. Springer. https://bookdown.org/edeftg/machine_learning_with_rust/measuretheory.html#sigma https://blog.naver.com/birth1104/221853268891