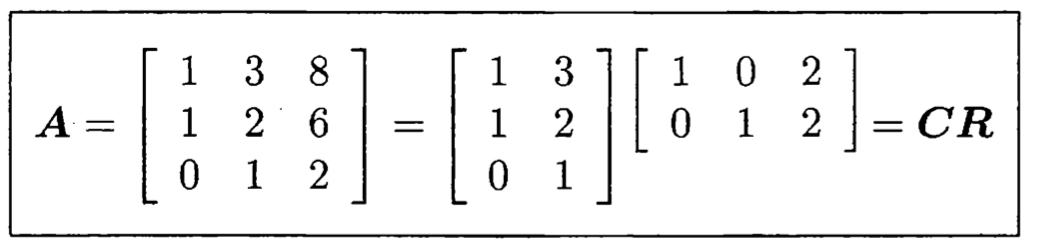Part I. Highlights of Linear Algebra

Posted Jan 31, 2024

$Preview Image$

By Gang Yong-Jin 36 min read

https://math.mit.edu/~gs/learningfromdata/

Part I에는 $Ax=b$, $Ax=\lambda x$, $Av=\sigma u$, factorization of $A$, 그리고 $Minimize \frac{\|Ax\|^2}{\|x\|^2}$ 에 대해 다룬다. (1p) 다른 건 선형대수 수업에서도 봤던 내용인데 $Minimize \frac{\|Ax\|^2}{\|x\|^2}$ 는 뭔지 잘 모르는 상태로 시작했다.

I.1 Multiplication Ax Using Columns of A

2023.12.29

내용

$Ax$ 는 $A$의 column들의 linear combination이다. 이게 fundamental

행렬 A와 벡터 x에 대해 column들의 linear combination으로 보는 것이 더 higher level이고 이는 Column Space로 이어짐. (2p)
$Ax=b$에서 $b$가 column space 안에 있을 때 solvable하다는 것, (linearly) independent 의 정의, $R^3$에서 independent column 3개가 있으면 invertible이라는 것 복습 (3p)
rank는 independent column의 개수를 세는 것 (4p)
A=CR (5p)
- $C$는 $A$의 column들 중 independent한 것들만 모은 것(이므로 A와 같은 column space를 가짐).
- 그리고 $R$은 $C$의 column들을 어떻게 조합해야 $A$가 나오는지에 대한 정보가 들어있는데, 이는 rref와 같음
- $A=CR$은 Fundamental Theorem of Linear Algebra의 첫 번째 파트 중 dim(C(A)) = dim(C(A^T)) = r 을 증명할 수 있음. (5p)
  - $C$에 $R$을 곱하는 게 $C$의 column들을 조합하는 것이듯 R에 C를 곱하는 것은 $R$의 row들을 조합하는 것과 같음. 따라서 $R$의 row들은 $A$를 구성하는 것들이고 independent하기까지 하니 $C(A^T)$의 basis들임.
  - 그래서 $C$의 column이 $C(A)$의 basis, $R$의 row들이 $C(A^T)$의 basis인데 (곱하기를 하려면) $C$의 column 개수 = $R$의 row개수 이니까 FTLA가 증명된다고 하는 것이 아닐지..
- SVD는 A=CR에서 C가 orthogonal column 을, R이 orthogonal row를 가지는 경우. (5p)

Problem Set I.1

17, 18번

I.2 Matrix-Matrix Multiplication AB

2024.01.01 ~ 2024.01.02

내용

$AB$ = Sum of Rank One Matrices

$AB$는 row vector와 column vector의 outer product 여러 개의 합으로 볼 수 있다 (9~10p)
- 이 rank one matrix 역시 $C(A) = C(A^T)$ 의 예시가 됨 (10p)
- Matrix Multiplication을 inner product 방식으로 하든 outer product 방식으로 하든, $(m\times n)\times(n\times p)$의 경우에 $mnp$번의 곱셈을 하고, 곱셈하는 숫자들은 같은데 순서만 다름 (10p) - inner product 방식: $mp$번의 내적을 하는데, 그 각각에는 $n$번의 곱셈. 총 $mnp$ - outer product 방식: $n$개의 outer product가 있는데, 그 각각에는 $mp$번의 곱셈. 총 $mnp$

행렬 A를 CR로 분해 후 각 col*row들에 대해 아는 것은 A의 largest piece를 관찰하는 것 (11p)

5개의 중요한 factorization: $A=LU, A=QR, S=QΛQ^T, A=XΛX^{-1}, A=UΣV^T$ (11p)
- S와 Q는 선형대수의 King가 Queen (11p)
예시: $QΛQ^T$를 유도한 후 각 $\lambda qq^T$가 rank one piece 라는 것을 보여줌 (11~12p) 한양대 선형대수 수업 자료에서도 나온 적 있었던 부분. 이제 이해함

* $AB$ 중 $B$의 row들은 b*으로 표기함: $b^T$로 표기하지 않는 이유는, 그러면 $B$를 transpose했을 때처럼 $b^T$를 $B$의 column들로 오인할 수 있어서. (12p)

Problem Set I.2

2024.01.02

1,6,8번

I.3 The Four Fundamental Subspaces

2024.01.02

내용

4 Subspaces에 대한 예시 3개가 제시됨.

Example 2: subspace의 basis들은 perpendicular인 게 좋다는 점 제시 (14p)
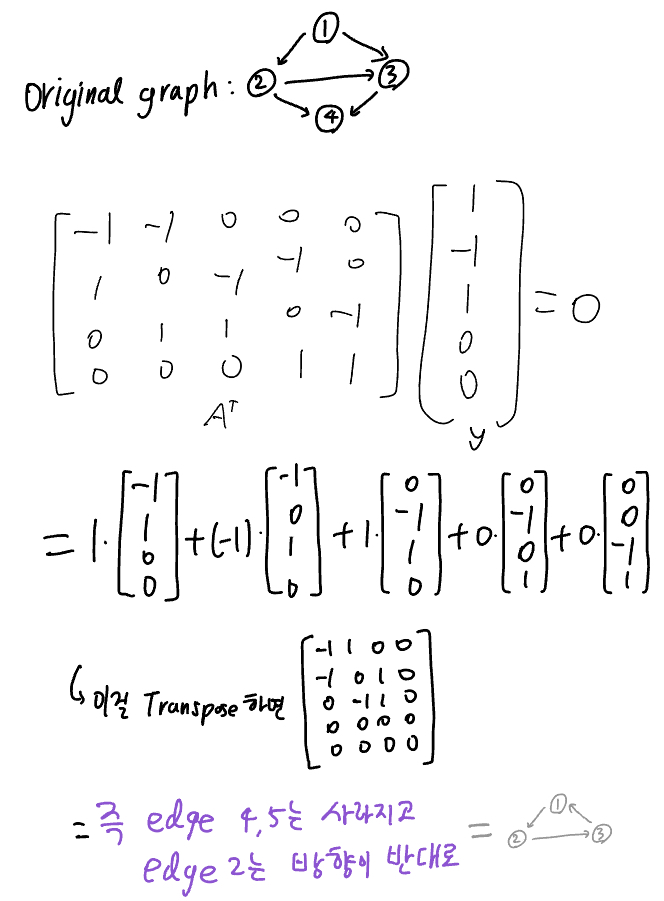
Example 3: 행렬 예시 자체가 그래프의 incidence matrix
- element가 -1이면 그 노드가 start node, 1이면 그 노드가 end node라는 뜻
- $A$는 $m\times n$ 사이즈이며 m개의 edge와 n개의 node를 나타냄
- 아래의 column space와 left null space구할 땐 $A^T⋅y=0$으로 만드는 $y$에 대해 논하는데 (17p)
  dependent rows→ $A$에 $y$를 곱한 결과는 그래프로 보면 loop
  independent rows → $A$에 $y$를 곱한 결과는 그래프로 보면 tree
- $N(A^T)$를 구할 때
  - $A$에 $y$를 곱한 게 그래프로 보면 loop이 되는 $y$를 찾으면 → $A^T⋅y=0$을 만족 (17p)
    이건 반대로 $A^T⋅y=0$ 인 $y$가 그래프에선 loop을 만든다는 순서로 풀어놓은 것이긴 함
- row가 서로 dependent인지 볼 때 elimination 말고 loop, tree로 보는 게 beautiful way (17p)
$AB$, $A+B$의 Rank에 대한 증명들 (19p)

Problem Set

I.4 Elimination and A = LU

2024.01.03 3:00 AM

내용

선형대수의 most fundamental problem은 $Ax=b$를 푸는 것이라고 제시 (21p)
이 파트의 핵심은 elimination 과정을 rank 1 matrix들의 관점에서 보는 것 (21p)
- 각 elimination은 행렬lu*를 없애는 것이고, 그 rank one matrix들의 합이 $A$.
LU 전에 2x2 $A$에 대해 $Ax=b$를 row picture로 보는 것부터 (Figure I.4) (21p)
(column picture는 figure 생략)
$n \times n$에서 $n≥3$ 이면 column picture로 보는 게 더 편함 (22p)
23p 윗부분은 그냥 LU decomposition의 과정

LU decomposition의 key idea: Reduce the problem size from n to n-1 by elimination (24p)
LU decomposition 역시 n개의 rank one matrix들의 합으로 볼 수 있다! (23~24p)

25p 윗부분은 LU로 Ax=b 구하는 법 (c벡터 사용해서)
- → 하나의 square system이 두 개의 triangular system으로 바뀜 (25p)
pivot은 0이 아니어야 한다! a_11=0이면 다른 row가 pivot row가 될 수 있을텐데, Good codes will choose the largest number to be the pivot, even if a_11 is not zero 라고 함
PA=LU (26p)

Problem Set

I.5 Orthogonal Matrices and Subspaces

2024.01.03 10:00 PM

내용

* Orthogonal matrices 라 하면 square with orthonormal columns 라 하는데.. 사실상 Orthonormal matrices 라고 하는 게 맞다고 함(29p)

Orthogonal matrix $Q$에 대해 $\|Qx\|=\|x\|$ (29p)
30p부터는 orthogonal한 vector, basis, subspace, matrix의 예시가 나옴
- orthogonal basis와 Hadamard matrix (30p)
- orthogonal subspaces의 예시는 4 fundamental subspaces (31p)
- SVD is most important theorem in data science; 단순 Gram-schmidt로 $A$의 $C(A), C(A^T)$를 찾는 것과 달리, SVD는 $v$와 $u$가 $Av=\sigma u$ 의 관계로 이어질 수 있게 함 (31p)
- Left inverse, Right inverse (32p)
- Projection Matrix $P$에 대해 $Pb$는 $b$를 $P$의 column space로 proejct한 것 (32p)
  - $P^2=P$이면 $P$는 projection matrix인데, $Q$에 대해 $P = QQ^T$는 projection matrix임
    $\because P^2=(QQ^T)(QQ^T)=Q(Q^TQ)Q^T=QQ^T=P$
    그래서 orthonormal한 column들로 이루어진 $Q$로 project할 때는 $P=QQ^T$를 사용 (32p)
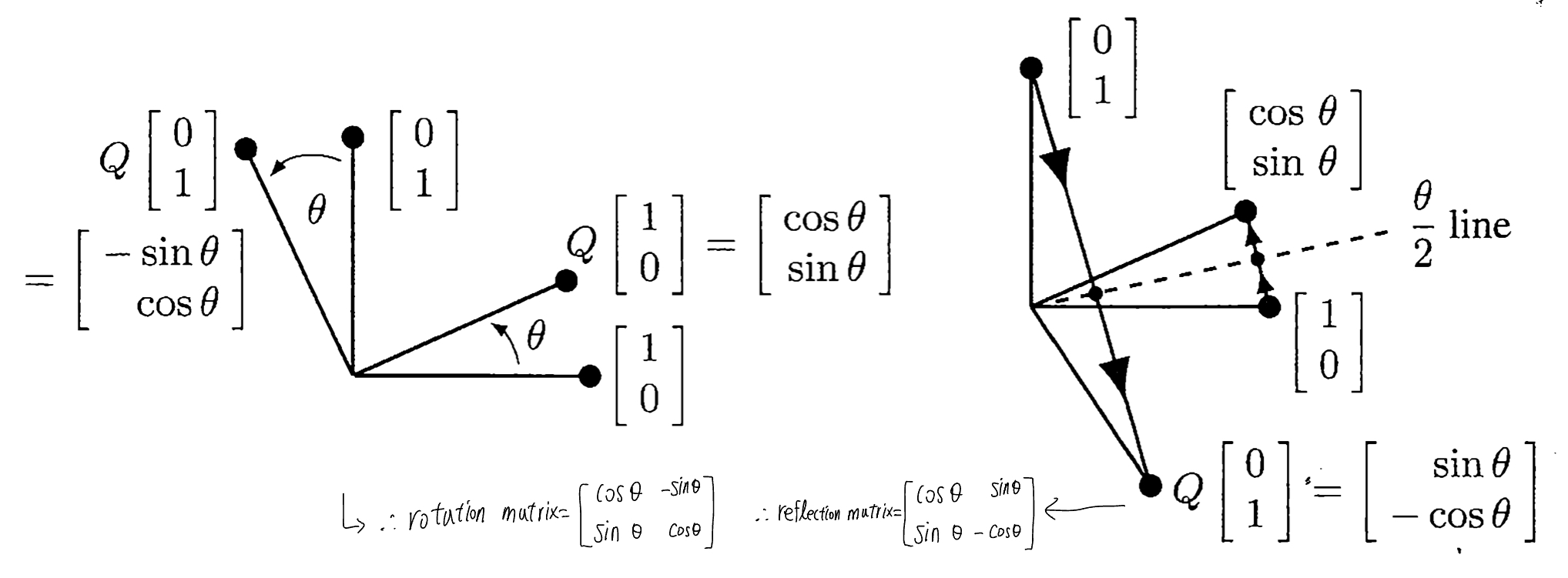
- orthogonal matrix 중에는 rotation matrix, reflection matrix도 포함 (33p)
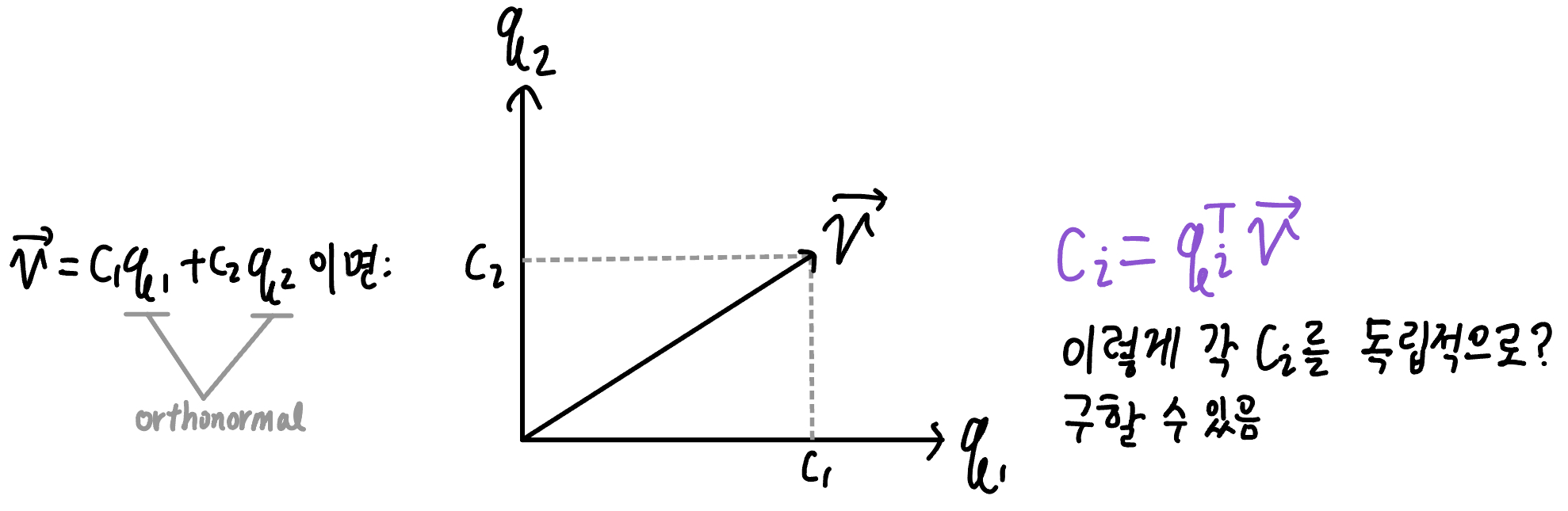
Orthogonal Basis = Orthogonal Axes in $R^n$
basis가 $q$이면 $v=c_1q_1+c_2q_2$ 의 $c$들을 separately 구할 수 있음
예시로 householder reflection (34p)

어휘..

hypotenuse
right triangle

Problem Set

1 (그냥 풀어봄), 4

I.6 Eigenvalues and Eigenvectors

2024.01.04 11:00 AM

내용

$n \times n$인 $A$에 $n$개의 eigenvector가 있을 때 $v = c_1x_1+...+c_nx_n$이다? (36p)
Similar matrix: $BAB^{-1}$ 은 $A$와 eigenvalue가 같다. (증명은 38p)
- 활용: $det(A-λI)$ 계산이 힘들 때 $BAB^{-1}$를 triangular로 만들어서 편하게 eigenvalue를 구함

(optional) Geometric Multiplicity, Algebraic Multiplicity로 diagonalizable 여부 판별하기 (40p)

Problem Set

I.7 Symmetric Positive Definite Matrices

2024.01.04 12:40 PM

내용

Symmetric Matrix의 특징: 1. real eigenvalue 2. can choose orthogonal eigenvectors. (44p)
Positive definite: powerful property that puts them at the center of applied mathematics
꼭 symmetric일 때만 해당되는 건 아닌 듯
positive definite이면 $AA^T$ 로 분해 가능 (90p)

positive definite인지 test하는 법 5가지:

Eigenvalue가 >0인지 열심히 확인
Energy-based definition: 가장 중요한 아이디어!! 이게 아래의 test들도 파생시킴 $energy = x^TSx>0\quad∀x≠0$ 이면 positive definite이다. (46p) 증명은 $Sx=\lambda x, \ \ x^TSx=\lambda x^Tx$. 즉 $x^TSx>0$이려면 우변에서 $\lambda>0$이어야 함.
ex) $S_1, S_2$ 모두 positive definite이면 $S_1+S_2$ 도 positive definite임을 energy test로 쉽게 검증
$S=A^TA$인데 $A$는 independent columns (dependent면 zero energy 유도 가능) (47p)
이게 Cholesky Decomposition이고, symmetric인 S에 대해 다음 방법 등으로 구할 수 있음
- $S=LDL^T$하고 나면 $A=\sqrt{D}L^T$
- $S=QΛQ^T$이니 $A=Q\sqrt{Λ}Q^T$
leading determinants(왼쪽 위에서부터 대각선으로 한 칸씩 확장) 모두 positive
elimination 후 모든 pivot들이 positive k-th pivot = $\frac{D_k}{D_{k-1}}$ (48p)

linear algebra의 positive definite matrix는 calculus의 minimum problem과 연결 가능 (49p)
- univariate일 때 특정 지점 $x_0$에서 $\frac{df}{dx}=0, \quad \frac{d^2f}{dx^2}>0$이면 minimum이듯
- multivariate일 때는 $(x_0,x_1,…,x_n)$에서 편미분값들=0, Hessian Matrix가 positive definite이면 최소. Hessian Matrix의 eigenvalue들을 비교하는 그 얘기 (49p)
- Hessian matrix의 eigenvalue들 중 양수 음수 다 있으면 saddle point 라는 건 미적2 기말고사 범위 첫 내용의 그것과 같은 듯 (50p)
- 또는 hessian이 positive definite(semidefinite)이면 함수는 convex, eigenvalue들이 특정 양수 $\delta$보다 크면 strictly convex
Optimization and Machine Learning: 이계도함수를 다 계산하는 건 어려움을 다시 강조 (50p)
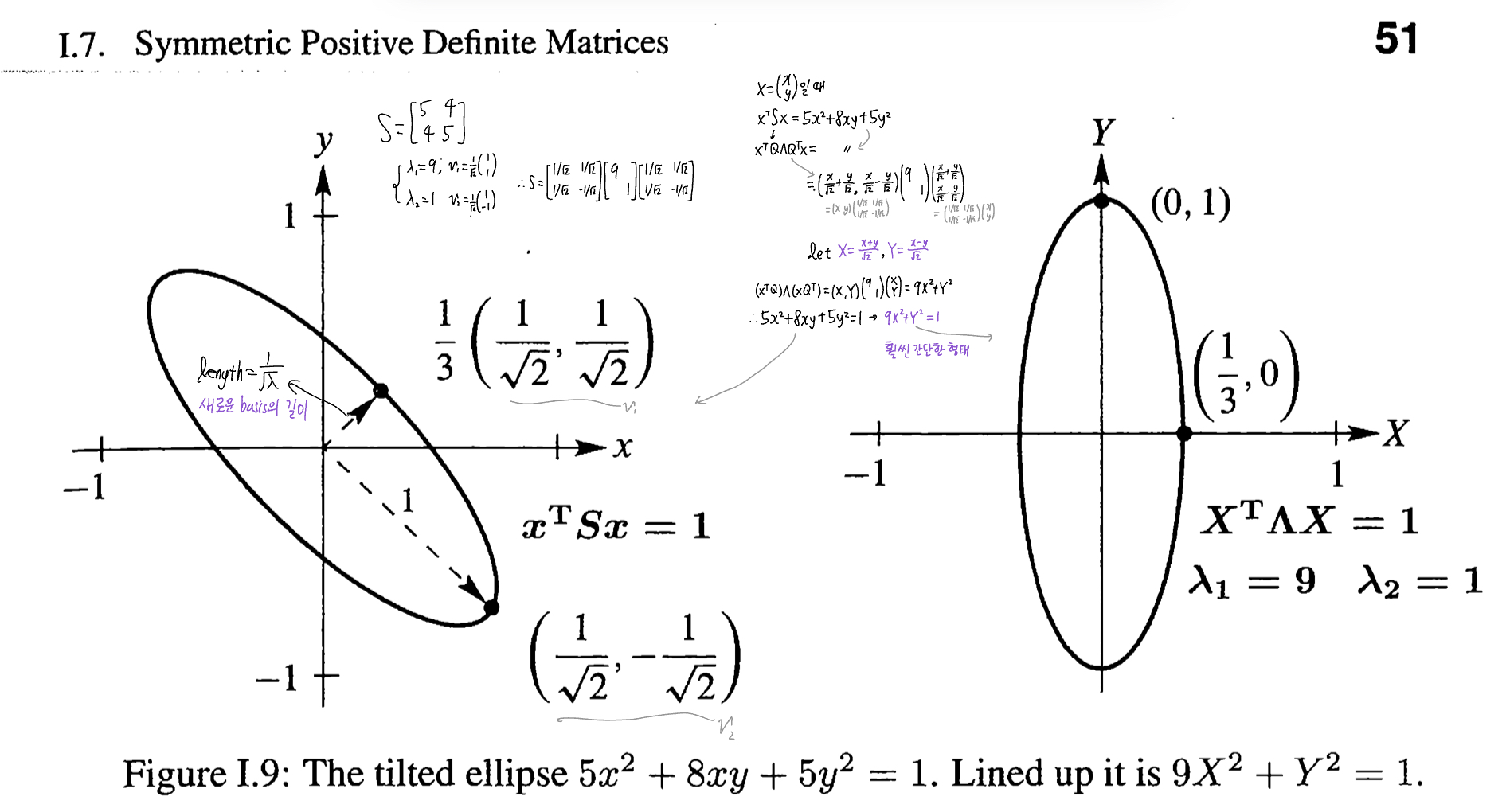
The Ellipse: 시작에 앞서.. 49p부터 나오던 $[\begin{matrix} 5 & 4\\ 4 & 5 \\ \end{matrix} ]$ 의 energy function $E(x,y)$에 대해
$E(x,y)=5x^2+8xy+5y^2>0$이 bowl opening upwards라는 말은 3차원에서 봤을 때를 말함
$S=QΛQ^T$는 principal axis theorem이라고도 함; $q$벡터들을 구하면 그게 새로운 axis로 쓰일 수 있음. (Figure I.9)

Problem Set

I.8 Singular Values and Singular Vectors in the SVD

2024.01.04 3:20 PM

내용

Reduced form of the SVD: rank 개수까지만 남긴 것 ((57p)
The Important Fact for Data Science: SVD도 다른 분해들처럼 행렬을 rank one pieces로 나누는데, SVD는 그 piece들이 중요한 순서대로 나타남. 첫 번째 piece $σ_1u_1v_1^T$가 가장 $A$와 가까움. (58p)
SVD 구하는 법과 proof가 있는데 읽고 넘김 (59p), 60p 예시도 생략

Q&A

$S$가 symmetric positive definite이면 $S=QΛQ^T=A=UΣV^T, \quad U=V=Q$ (61p)
$S=QΛQ^T$에서 negative eigenvalue가 있다면? → $σ$는 부호를 바꿔서 양수로, 대응하는 $u$는 부호를 바꿔서 음수로. (61p)
KL transform은 stochastic form of PCA (61p)
Geometry of SVD: $U,V$ 는 orthogonal matrix니까 rotation matrix로 볼 수 있다.(62p)
$V,Σ,U$순서로 rotate, stretch, rotate
$u_i,\sigma_i,v_i$ 를 하나하나 살펴보면 $maximize \frac{\|Ax\|}{\|x\|}$ 과 관련이 있음
1. 일단 maximize하는 $x$가 $v_1$이고, 이 때 $\frac{\|Ax\|}{\|x\|}=\sigma_1$ 가 나옴.
2. 그리고 저 다음으로 maximize하는 $x$를 찾기 위해 조건을 걸어서 $maximize \frac{\|Ax\|}{\|x\|}\quad s.t.\quad v_1^Tx=0$를 풀면 $x=v_2$임. $\frac{\|Ax\|}{\|x\|}=\sigma_2$ . (저 조건식 풀 때 lagrange multipler 사용)
3. 이런식으로 계속 찾다보면 (=ellipsoid의 axis들을 찾는) singular vector가 계속 나오는 것 (63p)
Singular vectors of $A^T$: $A^Tu_k=\sigma_kv_k$, 그냥 transpose 한 것 (64p)
A different symmetric Matrix also produces the SVD: $[\begin{matrix} 0 & A\\ A^T & 0 \\ \end{matrix} ]$로 한다는데 이건 무슨..? (64p)
$AB$와 $BA$는 같은 nonzero eigenvalue를 가진다: 그래서 $A^TA, AA^T$가 같은 singular value를 가짐 증명은 책에 있고.. (64p)
$maximize \frac{\|Ax\|}{\|x\|}$를 통해 $\|A\|=\sigma_1$라 했는데, 이를 통해 Submatrix B는 Matrix A보다 singular value가 더 클 수 없다는 것을 증명 가능. $\sigma_1(B)\le\sigma_1(A)$이고 $\|B\|\le\|A\|$ (65p)
SVD가 역사적으로는 행렬 말고 operator에 대해 먼저 나타났다고 함 (65p) $D(sinkt)=k(coskt)$ ← $Av=\sigma u$ 형태. ($D$=Derivative) - Derivative를 discrete하게 보면 finite differences이고 이로부터 $U,V$를 구하면 Discrete Sine Transform과 Discrete Cosine Transform을 얻을 수 있는데, 이게 JPEG기술의 핵심 (66p)
Polar Decomposition $A=QS=(UV^T)(V\Sigma V^T)$ (67p)

Problem Set

I.9 Principal Components and the Best Low Rank Matrix

2024.01.08 2:30 PM

내용

Principal Component라 함은 $U,V$ 의 column들인 $u_i, v_i$ 를 말하고, PCA는 가장 큰 $\sigma_i$들과 연결된 $u_i, v_i$를 사용해서 데이터 행렬에 담긴 정보를 이해하고자 함 (71p)
- $S=Q\Lambda Q^T$에서도 $Q$의 column들이 principal component여서 그걸 축으로 썼던 것과 같을 듯

일단 $A$와 가장 가까운 rank k matrix는 $A_k$라는 것에서 (모든 것은) 시작된다. (몇 가지 증명들이 있음) (71p)
Matrix norm $\|A\|$ 중 다음과 같은 세 가지 유명한 게 있음 (71p)
- Spectral norm: $max\frac{\|Ax\|}{\|x\|}=\sigma_1$ (aka $L^2$ norm, 또는 induced norm. $A$를 $Av$ 즉 벡터로 만들어서 vector norm으로부터 matrix norm을 유도했으니까)
  $A$ 가 벡터 $x$ 를 가장 길게 늘일 수 있는 정도를 찾는 것. 근데 그 값이 $\sigma_1$ 인 걸 SVD로 이미 알고 있음.
  $Av_1=\sigma_1u_1$인데 $v_1,u_1$은 어차피 unit vector이니 $\sigma_1$의 값이 어떤 벡터를 가장 길게 늘린 수치.
- Frobenius norm: $\|A\|_F=\sqrt{\sigma_1^2+\sigma_2^2+...\sigma_r^2}$
- Nuclear norm: $\|A\|_N=\sigma_1+\sigma_2+...\sigma_r$
- orthogonal matrix $Q$의 $\sigma_i=1$이다 (71p)
- 위 3종류의 norm에 대해 $\|Q_1AQ_2^T\|=\|A\|$
Eckart-Young에 대해 알아보자. If $B$ has rank $k$ then $\|A-B\| \gt \|A-A_k\|$ ..라는데 예시로 보면 (72p)
- $A = \begin{bmatrix} 4 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}$ 일 때, rank 2 matrix 중 가장 A와 가까운 $A_2 = \begin{bmatrix} 4 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$
  이다.
  Eckart-Young에 의해, ‘가장 값이 큰 두 수 4와 3을 남기자’ 하는 식으로 $A_2$를 선택하면 됨.
- 이 예시는 singular value가 4,3,2,1인 모든 $4 \times 4$ matrix에 대해 해당되는 이야기 ($L^2$ norm과 Frobenius norm은 $\|Q_1AQ_2^T\|=\|A\|$ 이니까.. 라고)
- 참고로 위의 $A,A_2$에 대해 error를 측정하면 $L^2$ norm으로는 2, Frobenius norm으로는 $\sqrt{5}$
다른 rank 2 matrix $B_2$ 가 아닌, 어쨌든 $A_2$ 가 best라는 얘기를 $L^2$ norm과 Frobenius norm에 대해 증명하는 듯 한데 건너뜀.
PCA: statistics, geometry, linear algebra의 측면에서 봄 (75p) centered data A에 대해, SVD 중 S의 column인 $u_1$ 의 방향이 closest line to the centered data인 이유는?
- **The Statistics Behind PCA** (or algebra, 76p) 1. Covariance matrix $S=\frac{AA^T}{n-1}$의 원소들이 variance/covariance라는 것과 2. 그 Covariance matrix $S$의 eigenvectors
  note: 데이터 A로부터 symmetric한 S를 구해내는 것보다 A에서 바로 SVD하는 게 더 빠르고 정확
- The Geometry Behind PCA 이건.. 그냥 $u_1$방향의 line이 data point들과의 수직거리 합이 가장 작아진다는 뜻. 증명 생략 (77p)
- The Linear Algebra Behind PCA
  - 데이터의 Total Variance를 Frobenius norm과 연결 가능. 이는 분산과 singular value를 연결하고, 이를 이용하여.. (78p)
  $i$ 번째 principal component $u_i$가 전체 분산 T 중 $\frac{\sigma_i^2}{T}$만큼을 설명(explain)한다고 해석
  - Eckart-Young Theorem에 의해 k개의 singular vector를 사용하는 게 다른 어떤 k개 벡터들의 조합보다도 데이터를 가장 많이 설명해낼 수 있다는 것이 알려짐. (78p)
    예를 들어 아래 그림은 k=1, m=2(# of feature)
effective rank: 몇 개의 singular value를 사용할지에 대한. scree plot으로 찾을 수도 있고.. (78p)
rank of quarter circle one-zero matrix

Problem Set

I.10 Rayleigh Quotients and Generalized Eigenvalues

2024.01.09 12:25 AM, 2024.01.09 3:10 PM

내용

Rayleigh quotient $R(x) = \frac{x^TSx}{x^Tx}$에 대해 $R(x)$의 최댓값은 $x=q_1$일 때 $R(x)=\lambda_1$. (eigenvalue 중 가장 큰 것. 반대로 eigenvalue 중 가장 작은 게 $R(x)$의 최솟값) $Sq_1=\lambda q_1$일테니 $R(x) = \frac{q_1^TSq_1}{q_1^Tq_1} = \frac{q_1^T\lambda_1 q_1}{q_1^Tq_1} = \lambda_1$ 이니까. (81p)
근데 $x=q_k$를 넣으면 그 지점들은 다 $R(x)$의 saddle points. (81p) 이건 왜 나온?
symmetric $S=A^TA$에 대해서 Rayleigh quotient는 A의 norm(의 제곱)과 같다. (81p) $\because ||A||^2=max\frac{||Ax||^2}{||x||^2}=max\frac{x^TA^TAx}{x^Tx}=max\frac{x^TSx}{x^Tx}=\lambda_1(S)=\sigma_1^2(A)$ 이걸 다르게 말하면, eigenvalue problem 역시 optimization임: Maximize R(x) (81p)

Generalized eigenvalues and eigenvectors: Applications in statistics and data science lead us to the next step.

Generalized symmetric eigenvalue problem이란: generalized rayleigh quotient $R(x)=\frac{x^TSx}{x^TMx}$와 같이 symmetric matrix $M$이 추가될 때 $Sx=\lambda x$가 아닌 $Sx=\lambda Mx$를 다루는 것. (82p)
- $M$: dynamical problem(역학 문제?)에선 mass/inertia matrix, statistics에선 covariance matrix.
- $Sx=\lambda Mx$에서 $H=M^{-1}S$로 두고 대입하면 $Hy=\lambda y$꼴이 나오고, 이 때의 $max \ R(x)=M^{-1}S$ (eigenvalue 중 가장 큰 것)이기는 한데.. 근데 이러면 $H$가 항상 symmetric이란 보장은 없음. (not really perfect, 82p)
- $H=M^{-\frac{1}{2}}SM^{-\frac{1}{2}}$ 이렇게 정의하면 eigenvalue들은 여전히 같은데도 $H$ 가 symmetric임! (82p) $M$이 positive definite이면 언제나 positive definite square root도 가진다 $M$은 symmetric이니까 $M=Q\Lambda Q^T$로 분해하면 $M^{-\frac{1}{2}}=Q\Lambda^{\frac{1}{2}}Q^T$로 구하면 됨. - 이제 $x=M^{-\frac{1}{2}}y$라고 두면, $\frac{x^TSx}{x^TMx}=\frac{y^T(M^{-\frac{1}{2}})^TSM^{-\frac{1}{2}}y}{y^Ty}=\frac{y^THy}{y^Ty}$가 돼서 $Hy=\lambda y$라는 ordinary symmetric problem으로 바꿀 수 있음. 그럼 $max \ \frac{y^THy}{y^Ty} = \lambda_1$.
- 결국: $M$이 positive definite일 때 $max \ R(x)=M^{-1}S$, which is largest eigenvalue.
- Example 1: 단순 계산. mechanical engineering이면 $\lambda$가 스프링의 frequency와 관련… (83p)
- Generalized eigenvector : symmetric이면 eigenvector끼리 orthogonal이듯, $Sx=\lambda Mx$로 확장하면 M-Orthogonal 이라는 개념이 나온다. (83p)
  $x_1^TMx_2=0$(M-Orthogonal) if $Sx_1=\lambda Mx_1$ and $Sx_2=\lambda Mx_2$ and $\lambda_1\ne\lambda_2$
$M$이 positive semidefinite으로 not invertible인 경우에는 $x_1^TMx_2=0$ 이 될 수 있어서 $$frac{x^TSx}{x^TMx}$의 값이 **무한대**가 될 수 있음. 이 때$M^{-\frac{1}{2}}$$과 $H$는 존재 불가.. (84p)
mathematical하게 보는 한 가지 방법은, $\alpha Sx = \beta Mx$, $\lambda=\frac{\beta}{\alpha}$로 두고 케이스를 나누는 것. $\alpha=0$일 때 $\lambda$는 무한대거나 undetermined일 수 있는데, 데이터 샘플이 # of features보다 적을 때 발생. → 그래서 $M$이 추가된 경우까지 커버하기 위해 아래의 GSVD라는 것이 나옴
Generalized SVD: (85p) column 수가 같은 두 tall thin matrices $A$와 $B$에 대해 $A=U_A\Sigma_AZ, \ B=U_B\Sigma_BZ$로 분해. 이 때 $A^TA=Z^T\Sigma_A^TU_A^TU_A\Sigma_AZ=Z^T(\Sigma_A^T\Sigma_A)Z$ 와 같이 가능해서, $S=A^TA$ 와 $M=B^TB$ 모두 $Z$ 로 diagonalize 가능함.
Fisher’s Linear Discriminant Analysis (86p)
- PCA처럼 Dimensionality reduction을 위한 테크닉
- Fisher’s criterion이라고도 하는, Separation ratio라는 것이 있다. $m_1, m_2$가 population1, population2의 feature들의 mean값들을 모은 벡터일 때 $R=\frac{(x^Tm_1-x^Tm_2)^2}{x^T\Sigma_1x+x^T\Sigma_2x}=\frac{x^T((m_1-m_2)(m_1-m_2)^T)x}{x^T(\Sigma_1+\Sigma_2)x}$ 즉 $\frac{x^TSx}{x^TMx}$의 형태로 풀어낼 수 있음. 이 ratio 값을 가장 크게 하는 $x$값인 $v$를 찾으면 - $v$와 수직인 plane이 두 population을 분리하는 것이고 - $v$벡터 방향의 line을 사용해서 차원축소를 할 수도 있고 (맞나?)

Problem Set

I.11 Norms of Vectors and Functions and Matrices

2024.01.11 12:00 AM, 2024.01.11 3:30 PM, 2024.01.12 2:00 AM, 2024.01.13 8:16 PM, 2024.01.14 1:43 PM, 2024.01.15 3:00 PM

내용

vector에 대한 것이든, function에 대한 것이든, matrix에 대한 것이든.. norm은 두 성질을 공유함 (88p)
- rescaling: $\|ku\|=\lvert k \rvert \|u\|$
- triangle inequality: $∥u+v∥≤∥v∥+∥u∥$
- $v=0 \Longleftrightarrow \|v\|=0$ 도 조건으로
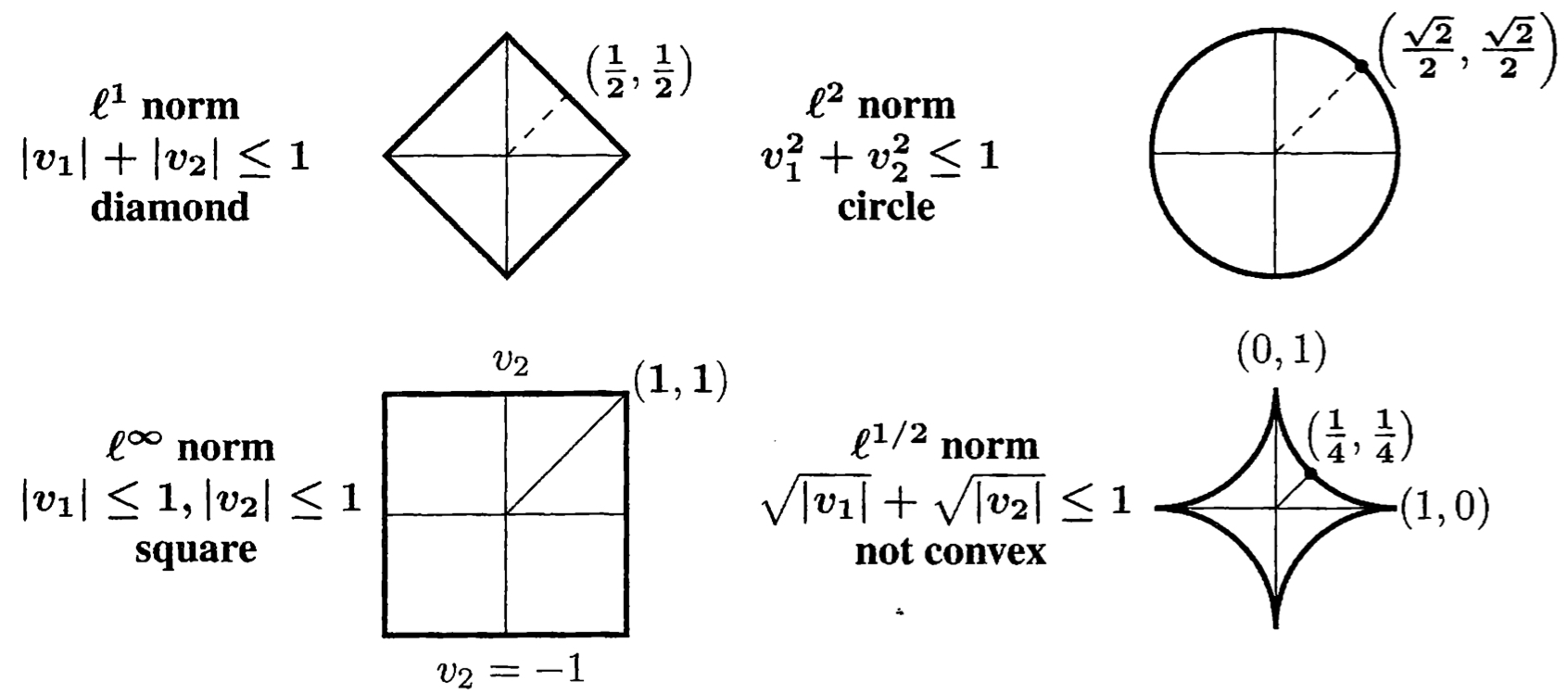
가장 중요한 세 가지 norm (88p)
- L2 norm: $\|v\|_2 = \sqrt{\lvert v_1 \rvert^2 + \lvert v_2 \rvert^2 + ... + \lvert v_n \rvert^2}$
- L1 norm: $\|v\|_1 = \lvert v_1 \rvert + \lvert v_2 \rvert + ... + \lvert v_n \rvert$
- max norm: $\|v\|_\infty=max \ of \ \lvert v_1 \rvert, ... , \lvert v_n \rvert$ ($l^\infty$ norm이기도 함)
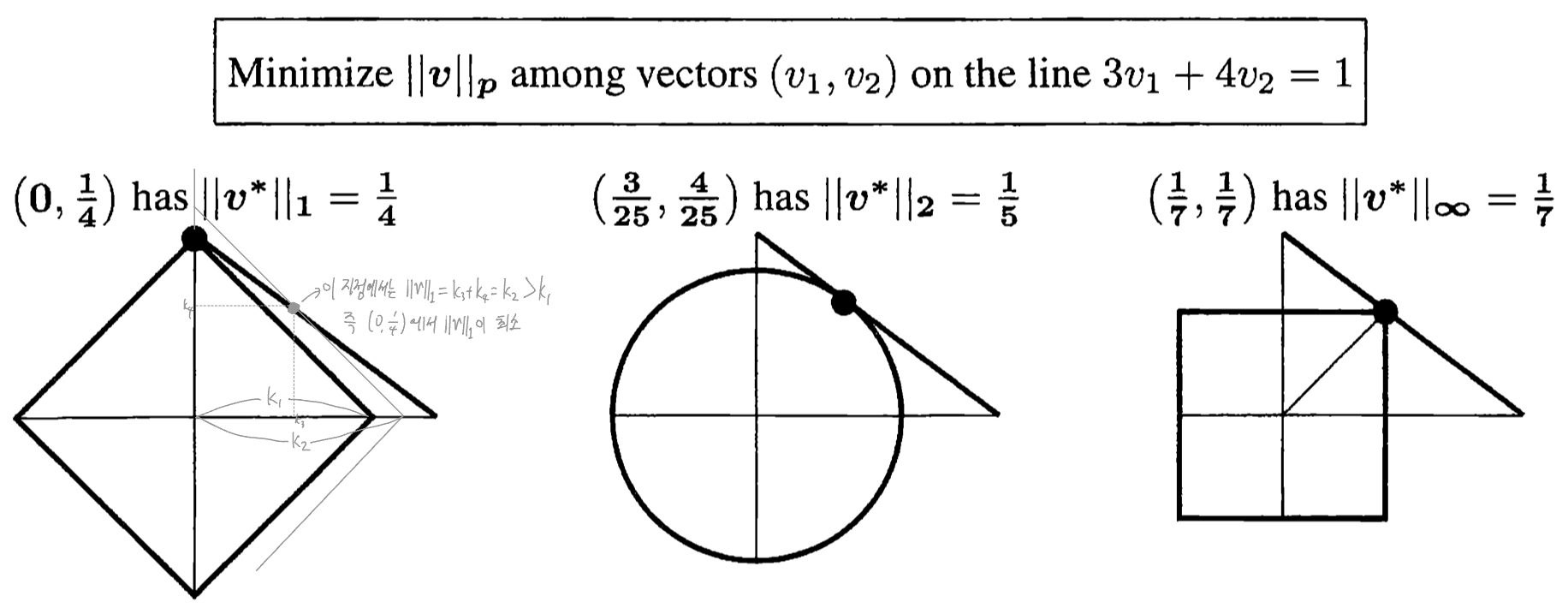
The Minimum of $\|v\|_p$ on the line $a_1v_1+a_2v_2=1$ (89p)**
- L1 norm: solution vector $v^*$이 sparse함
L0 norm: zero norm=그 vector의 element들 중 nonzero인 것이 몇 개인가? (89p)
Inner Products and Angles (90p) Cauchy-Schwarz inequality와 triangle inequality는 most important inequalities in mathematics 그리고 L2 norm이 위의 두 inequality와 관련이 있음 (둘 다 dot product와 연관이 있으므로)
Inner Products and S-Norms (90p) 다른 norm과 연관시킬 수 있는 다른 inner product도 있음 positive definite matrix $S$에 대해 $\|v\|_S^2=v^TSv$를 S-norm이라 하고, $(v,w)_S=v^TSw$를 S-inner product라 하는 것. 그러면 $S=A^TA$이므로 $v^TSw=v^TA^TAw=(Av)^T(Aw)$. 즉 weight된 벡터들의 내적. Einstein and Lorentz? (91p)
Norms and Inner Products of Functions (91p)
- function $f(x)$가 vector in function space이고 function간의 linear combination이 가능하다? vector를 함수처럼 쓰려는 게 핵심 아이디어
- vector의 element 개수가 무한한 infinite dimension일 때는 마지막 element들이 쭉 0이면 incomplete?
- Banach Space, Hilbert Space (91p) $\ell^1, L^1,\ell^{\infty}, L^{\infty}$: Banach space, $\ell^2,L^2$: Hilbert space
Smoothness of Functions (92p)
- function space $C[0,1]$이라 하면, $C[0,1]$은 구간 [0,1]에서 연속인 모든 함수들을 모은 것을 말함.
- function space $C$는 smoothness의 정도가 같은 함수들을 모음.
  - $C^n$은 1~n계 도함수가 연속인 함수들을 모은 것. $C^{\infty}$ 은 무한 번 미분 가능한 함수들을 모은 것.
  - 미적분학이나 기하학에서의 매끄러움은 $C^1$정도로 매끄러우면 된다. 즉, $f$가 미분 가능하고 $f'$이 연속이면 된다.
  - 해석학, 함수해석학에서는 매끄러운 함수란 (높은 확률로) $C^{\infty}$ 의 원소(인 함수)를 말한다.
- function space에서의 max norm $\|f\|_C=max \lvert f(x) \rvert$ ($f$가 주어진 구간에서 연속일 때)
- $C^k$ norm: $\|f\|_{C^k}=\sum_{i=0}^{k}{\|f^{(i)}\|_{\infty}}$이고 $C^k$ norm은 Banach Space (+ not Hilbert space)
- $L^2$ space 기반으로 만들면 $\|f\|_{H_1}^2=\|f\|^2+\|\frac{df}{dx}\|^2$ 이렇게 Hilbert space $H^1$을 만들 수 있음
Norms of Matrices: The Frobenius Norm (92p)
- space of matrices는 vector space의 rule들을 다 따름. 따라서 matrix norm도 vector norm의 세 규칙을 따르고, 하나가 추가됨
  $\|A\|>0 \ when \ A\ne0 \ matrix, \|cA\|=|c|\|A\|,\|A+B\|\le\|A\|+\|B\|$ 그리고 $\|AB\|\le\|A\| \ \|B\|$ - 참고로 마지막의 경우 rank-1 matrix는 $\|ab^T\|=\|a\| \ \|b^T\|$로 등식이 됨
- orthogonal matrix $Q$에 대한 성질 복습: $\|Qx\|_2=\|x\|_2$, $\|QB\|_F=\|B\|_F$ (93p)
  그래서 $\|U\Sigma V^T\|_F=\|\Sigma\|_F=\sqrt{\sigma_1^2+...+\sigma_r^2}$
  (이것 덕분에 $\|A\|_F=\sqrt{\sigma_1^2+...+\sigma_r^2}$ 가 유도되는 것. 심지어 $\|A\|_F^2=trace(A^TA)$)
- trace를 이용해 Frobenius norm의 제곱은 그 행렬의 모든 원소 각각의 제곱의 합과 같음을 유도 가능
- matrix norm은 $A$를 $v$에 곱했을 때 얼마나 변화했는지, 즉 largest growth factor를 구하는 것
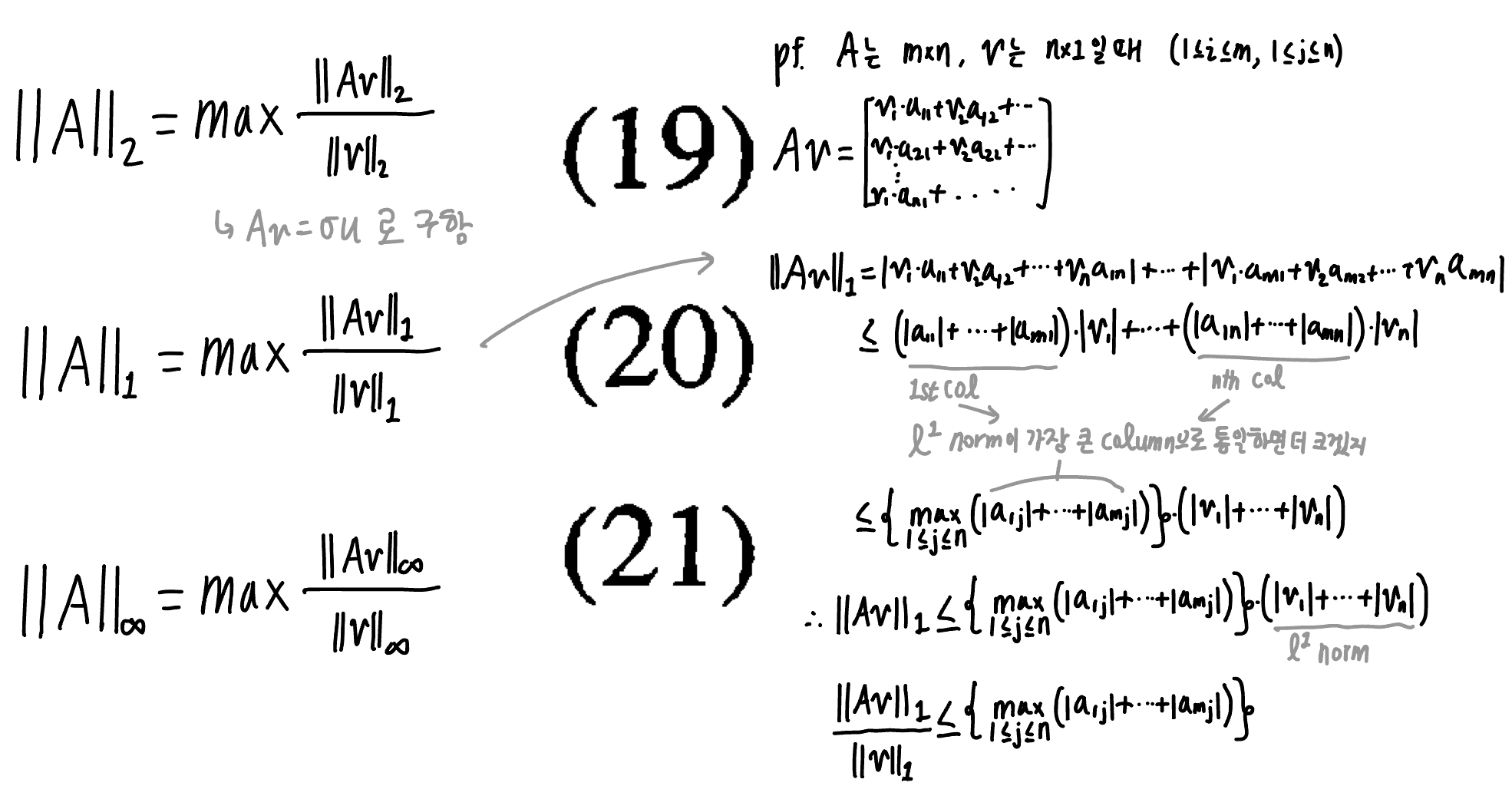
  - $\|Av\| \le \|A\| \ \|v\|$이런 식으로 식을 세우면 성립한다는 점 ($\because ||A||$가 변화량 중 가장 큰 값, 즉 $||Av||$의 값들 중 가장 큰 것과 값은 값으로 고정된 값이고, $||Av||$는 $v$에 따라 변화하는 값이니까) 을 통해서도 $\|AB\|\le \|A\| \ \|B\|$ 증명 가능 (94p) 참고로 $\|Av\| \le \|A\| \ \|v\|$ 을 통해서 행렬의 $l^1, l^{\infty}$ norm 값을 유도함
  - $\|A\|_2, \|A\|_1, \|A\|_{\infty}$ 각각을 구하는 법은:
    - 이유는? l2 norm은 뭐 SVD고 (그래서 l2 norm의 값은 $U, V^T$에 영향을 받지 않음.) l1 norm:
      
      l infinity norm은.. 생략
      l1, l infinity norm 구하는 법에 대한 증명 ¹
  - 아래 l1과 l infinity norm의 연관: $|A|_{\infty}=|A^T|_1$ , 이를 활용해 l1, l2, l infinity norm의 관계 유도 가능: $ A _2^2= A _1 \ A _{\infin}$ (94p)
The Nuclear Norm (trace norm) (95p) « I.9 에서도 나온 적 있음
- $\|A\|_{nuclear}=\sigma_1+...+\sigma_r$ .
- III.4에서 나오는 결측치가 있을 때의 matrix completion에서 nuclear norm이 key가 됨
- medical norm: $\lvert \lvert \lvert A \rvert \rvert \rvert _{\infty}$
Spectral Radius (95p)
- eigenvalue 중 가장 큰 것. $\lvert \lambda \rvert _{max}=max \lvert \lambda_i \rvert$. norm의 조건은 충족 못함
- 이게 중요한 이유는 $\lvert \lambda \rvert _{max}<1$일 때 $\|A^n\|\rightarrow0$ 이기 때문

Problem Set

2024.01.15

I.12 Factoring Matrices and Tensors: Positive and Sparse

2024.01.15 5:18 PM, 2024.01.30 4:10 AM

내용

data matrix의 factorization에 대한 wider view를 제시

$A=U\Sigma V^T$만으로 충분하지 않을 수 있는 케이스: nonnegative, sparse, tensor data (97p)
- sparsity: nonzero인 수들에 의미가 있다는 걸 알 수 있음.
- nonnegativity: meaningful한 수를 찾기 위해. 아래 참고
- 그래서 위 둘은 very valuable properties라고 함(98p)
- 그런데 SVD를 하면 보통 +,- 부호가 섞여있는 작은 값의 수들이 매우 많게 됨.
$\Sigma$를 $U$로 합쳐서 $A=UV$로 분해하는 아이디어? k-means와도 관련이 있다고
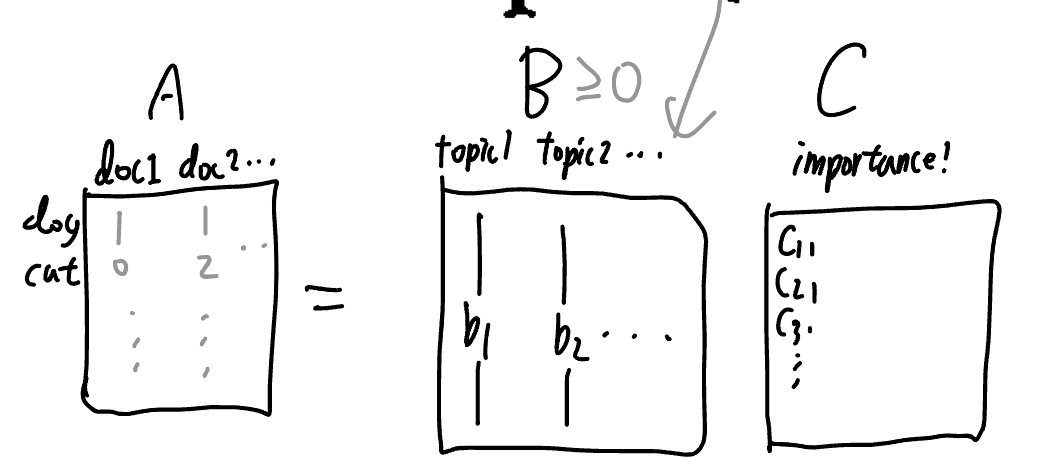
Nonnegative Matrix Factorization (NMF): $A\approx UV$(97p)
- 행렬 $A\ge0$ 을 lower rank이면서 negative entry가 없는 두 행렬 $U\ge0,V\ge0$로 분해하는 것.
  - 참고로 $A\ge0$인 행렬의 예시는 98p의 얼굴 이미지 데이터. 이미지 각 픽셀의 intensity가 행렬의 element이니 각 값은 0이상.
  - 왜 lower rank? → simplicity
  - 왜 nonnegative? → meaningful한 숫자들을 만들기 위함. plus-minus cancellation 없는! (무게, 부피, 개수, 확률 같은 것들도 다 양수죠?)
- $A\ge0$이 symmetric positive definite이면? $A=B^TB$ 분해는 가능할텐데, 보통 $B$가 nonnegative로 존재하지는 않는다. 보통은 그냥 $A$ 와 가장 가까운 $B^TB$를 찾아야 함. (97p)
- practical하게는, $U$ 와 $V$의 orthogonality를 포기해야 함. (sparsity, nonnegativity를 더 중시, 98p)
- 이건 SVD와 달리 NP-Hard problem임 (99p)
SPCA $A\approx BC$(98p)
- $A\approx BC$를 찾는데.. $B,C$는 뭐 특별한 건 아님. $A$의 column $a_j=c_{1j}b_1+...+c_{nj}b_n$ 이니 이게 더 등식에 가까울수록 더 좋은 $B,C$인 것.
- $C$의 column 개수 < $A$의 column 개수이다? 그럼 dimensionality reduction.
- 이걸 쓰는 예시가 Facial feature extraction, Text Mining/Document Classification (98p)
Optimality Conditions (99p)
- $\|A-UV\|_F, \|A-BC\|_F$ 의 값을 minimize하는 게 중요한데.. 이 내용은 잘 모르겠는
Computing the Factors: Basic Methods (99p)
- 어쨌든 $U,V$ 또는 $B,C$를 어떻게 계산해서 구할지가 문제
- alternating factorization: 두 행렬 중 하나를 고정 후 다른 하나를 optimize, 그 후 반대로. 이걸 반복 Frobenius norm을 사용해서 각 단계는 least square의 형태가 됨
- 근데 이 방법은 convergence가 보장되지 않음. III.4에서 발전된 형태 ADMM이 나옴 (99p)
Sparse Principal Components (99p)
- nonzero component가 너무 많으면 다뤄야 할 변수가 너무 많다는 것인데.. 그래서 non zero component의 개수가 중요.
- 근데 SVD는 $u,v$ 안에 대부분의 숫자가 다 nonzero임. 값이 너무 작은 걸 없앨 수도 있겠지만, 그냥 sparse vector를 만드는 알고리즘들이 제안되었음.
- matrix $X$에 대해서는 $l^1$ norm 말고 nuclear norm $\|X\|_N$ 을 사용.
- $l^1$ + ridge regression
Tensors (101p)
- tensor는 row, column에 이어 tube추가
- Example 2 : $w=Av$ 에서 $T_{ijk}=\frac{\partial w_i}{\partial A_{jk}}=v_k\delta_ij$ (101p)
  - 이 때 $Av$의 $A$는 딥러닝 레이어 하나의 weight matrix를 생각하면 됨.
- Example 3 : The Joint Probability Tensor (102p)
The Norm and Rank of a Tensor (103p)
- 3차원 텐서를 3-way tensor, tensor of order 3라 함
- Frobenius norm처럼 norm of T = $sum T^2_{ijk}=\|T\|^2$
- 텐서의 의미: 이것도 matrix처럼 linear operator가 되거나, RGB 이미지는 3-way, 영상은 4-way tensor.
- tensor의 factorization은 다루지 않고, rank of tensor도 간단하지 않음 (103p)
- Eckart-Young theorem이 있는 matrix와 달리, tensor는 어떤 tensor에 대한 best approximation이 존재하지 않음. 그럼에도 low rank tensor를 구하는 방법에는 CP, Tucker가 있음
CP Decomposition (104p)
- 여전히 핵심은 rank-1 tensor의 합으로 텐서 T를 approximate하는 것
- SVD와 달리 각각이 orthogonal하지 않음.
- NP-Hard
- 이것도 alternating algorithm 있음 (105p)
- 목표는 $T \approx a_1\circ b_1\circ c_1+...+a_R\circ b_R\circ c_R$
Matricized Form of a Tensor T (105p)
- CP Decomposition 하기 전에 tensor를 matricize하는 방법 소개
- 위의 각각이 $T_1, T_2, T_3$
The Khatri-Rao Product $A\odot B$ (105p)
- Kronecker product를 이용해서, $K \times R$과 $J \times R$을 곱하면 $JK \times R$이 나오는…
- column들이 $a,b,c$인 행렬을 각각 $A,B,C$라 하면 $T_1 \approx A(C \odot B)^T, T_2 \approx B(C \odot A)^T, T_3 \approx C(B \odot A)^T$ 와 같이 나타낼 수 있음
Computing the CP Decomposition of T (106p)
- $B,C$ 고정 후 $A$에 대한 least square 풀고, … , 를 반복. 자세한 과정 생략 (107p)
The Tucker Decomposition (107p)
- $T \approx \Sigma^{P}_{1} \Sigma^{Q}_{1} \Sigma^{R}_{1}g_{pqr} a_p \circ b_q \circ c_r$ .
- 이제는 Khatri-Rao 말고 Kronecker product 사용: $T_1 \approx AG_1(C \otimes B)^T$, 역시 생략
Decomposition and Randomization for Large Tensors (108p) 생략

Problem Set

References

Strang, G. (2019). Linear Algebra and learning from data. Wellesley-Cambridge Press.

https://pasus.tistory.com/34 ↩

Mathematics, Linear Algebra (Linear Algebra and Learning from Data)

Linear Algebra

This post is licensed under CC BY 4.0 by the author.

I.1 Multiplication Ax Using Columns of A

내용

Problem Set I.1

I.2 Matrix-Matrix Multiplication AB

내용

Problem Set I.2

I.3 The Four Fundamental Subspaces

내용

Problem Set

I.4 Elimination and A = LU

내용

Problem Set

I.5 Orthogonal Matrices and Subspaces

내용

어휘..

Problem Set

I.6 Eigenvalues and Eigenvectors

내용

Problem Set

I.7 Symmetric Positive Definite Matrices

내용

Problem Set

I.8 Singular Values and Singular Vectors in the SVD

내용

Problem Set

I.9 Principal Components and the Best Low Rank Matrix

내용

Problem Set

I.10 Rayleigh Quotients and Generalized Eigenvalues

내용

Problem Set

I.11 Norms of Vectors and Functions and Matrices

내용

Problem Set

I.12 Factoring Matrices and Tensors: Positive and Sparse

내용

Problem Set

References

Trending Tags