Repeated Game
Repeated Game
여전히, Prisoner’s dillema에서 두 player가 모두 자백하지 않는 경우가 왜 균형점이 될 수 없는지에 대해 설명할 방법이 없다. Repeated game에서는 Stage game을 여러 번 반복하는 경우를 가정해 더 다양한 상황에 대해 논의한다.
Finitely Repeated Game
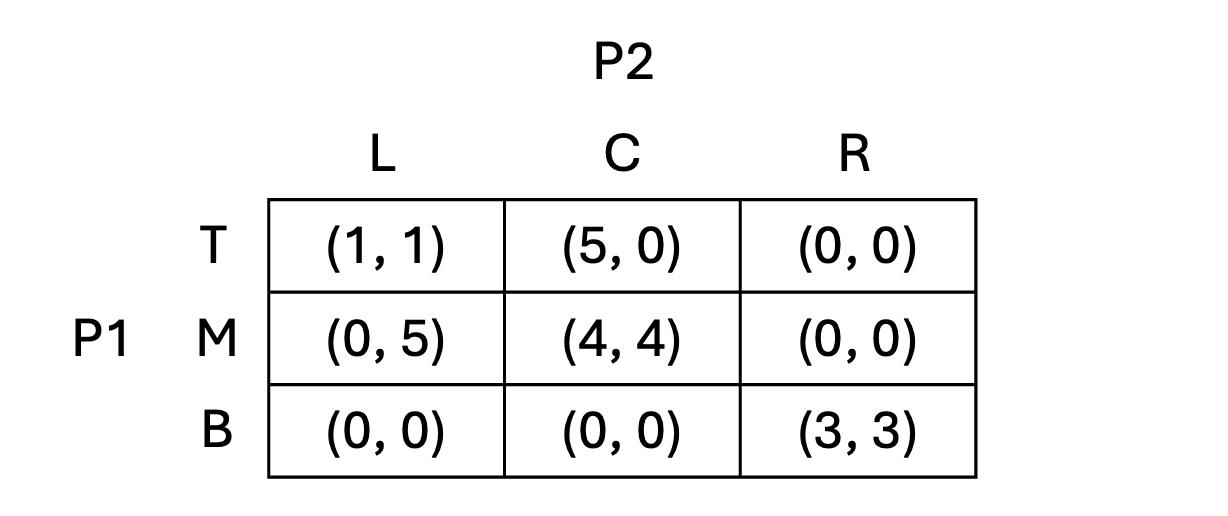
- 위 game의 N.E.는 (T, L), (B, R) 이다.
- Reward와 Punishment의 개념이 생긴다.
- 예를 들어, 첫 period에서 (M, C)가 성사되었다면 다음 period의 첫 player는 B/R을 선택하고, 성사되지 않았다면 T/L을 선택하는 전략을 취할 수 있다.
- 다만 Prisoner’s dillema에는 N.E.가 한 개이므로 reward/punish를 할 수도 없다.
Infinitely Repeated Game
이제 무한히 반복되는 게임을 가정한다. 보통 효용함수로는 \(U_i(s) = (1-\delta)\sum_{t=1}^{\infty}\delta^{t-1}u_i(a^t(s))\) 를 사용하는데, 이유는 아마 무한 급수의 합을 계산할 때 분모에 생기는 \((1-\delta)\)를 소거하기 위함으로 생각된다.
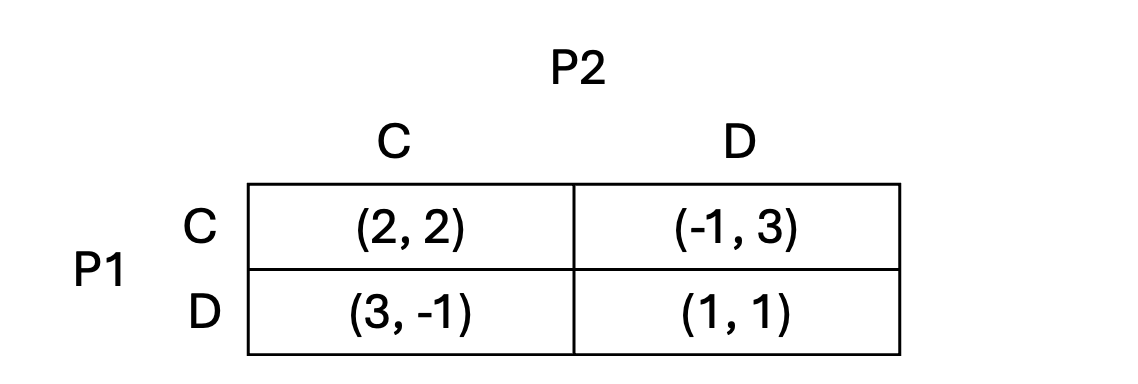
이하의 예시에서는 다음 game을 이용한다. N.E.는 (D, D)이지만, (C, C)가 양쪽 모두에게 더 이득이 되는 상황이다.
Trigger strategy
상대방이 이전 period에서 D를 선택했을 경우 $K$ step동안 D를 선택하다가, 그 이후에는 다시 C를 선택하는 전략이다. 상대방이 period 1에서 D를 선택한다면, 상대방의 Payoff는 다음과 같이 계산된다.
\[\begin{aligned} U_i((D, \sigma_i^t), \sigma_j^t) &= (1-\delta)(3 + \delta \cdot 1 + \delta^2 \cdot 1 + \cdots + \delta^K \cdot 1 + \delta^{K+1} \cdot 2 + \cdots) \\ &= (1-\delta)(3 + 1\cdot\frac{(1-\delta^K)}{1-\delta} + 2\cdot\frac{\delta^{K+1}}{1-\delta}) \\ &= 3(1-\delta)+ (1-\delta^K) + 2\cdot\delta^{K+1} \\ \end{aligned}\]만약 두 player가 모두 항상 C만 선택한다면, payoff는 아래와 같이 2가 된다.
\[U_i(\sigma_i^t, \sigma_j^t)=(1-\delta)\frac{2}{1-\delta}=2\]즉, \(2 \ge 3(1-\delta)+ (1-\delta^K) + 2\cdot\delta^{K+1}\) 이면 상대방은 D로 deviate하지 않을 것이다. 부등식의 성립 조건은 $K$의 값에 따라 달라진다.
이 때 $\frac{\partial \bar{\delta}_K}{\partial K}$ 의 관계가 성립한다. 즉, 처벌 강도 $K$가 커지면 $\delta$가 더 작은(=참을성이 더 약한) player의 마음도 돌릴 수 있다.
Grim Trigger
$K=\infty$인 경우를 말한다.
2024.06.23