Notations, PSNE, MSNE, THPE
2024년 1학기 ECO2035 게임이론과응용 수업 수강 내용을 정리
Strategic Form Game
Notations
- \(N = \{1,2,...,N\}\)
: A set of players - \(S_i \ \text{where} \ i \in N\)
: $i$’s starategy space \(u_i = \prod_{k \in N} S_k \rightarrow \mathbb{R} \ \text{where} \ i \in N\)
: $i$’s payoff function- \(S := \prod_{k \in N} S_k, \ S_{-i} = \prod_{k \ne N} S_k\) \(\quad\)
Definition (Strategic Form Game)
An n-player strategic (normal) form game $G$ is an $n$-tuple \(\{(S_1,u_1),...,(S_n,u_n)\}\).
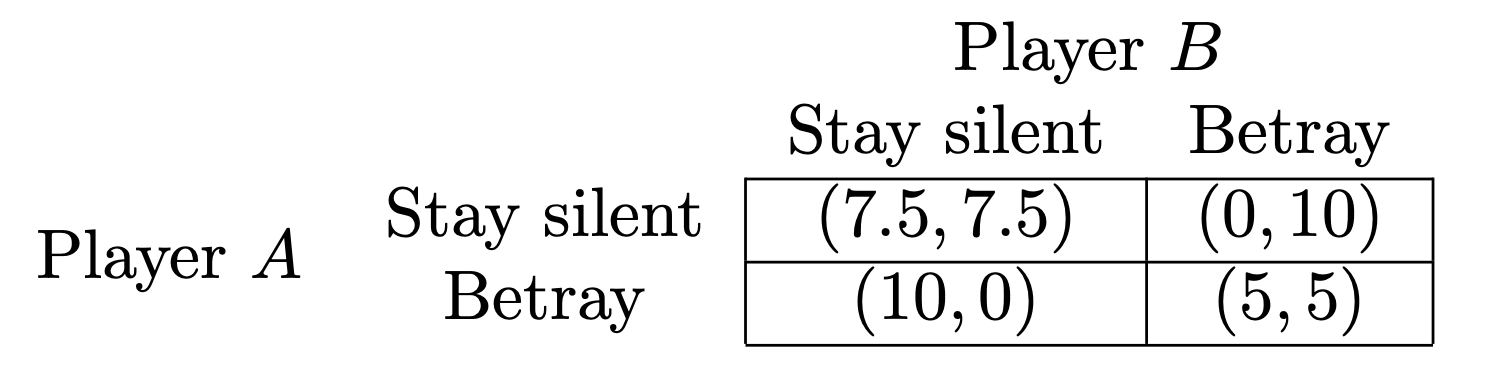
Example (Prisoner’s Dilemma)
- \(N = \{1,2\}\) \(\quad\)
- \(S_A = S_B = \{\text{Stay silent, Betray}\}\) \(\quad\)
- Payoff:
- \(u_A(\text{Stay silent, Stay Silent})=u_B(\text{Stay silent, Stay Silent})=7.5\) \(\quad\)
- \(u_A(\text{Stay silent, Betray})=u_B(\text{Betray, Stay Silent})=0\) \(\quad\)
- \(u_A(\text{Betray, Stay Silent})=u_B(\text{Stay silent, Betray})=10\) \(\quad\)
- \(u_A(\text{Betray, Betray})=u_B(\text{Betray, Betray})=5\) \(\quad\)
Remark: 이 상황에서 (Stay silent, Stay Silent)가 아닌 (Betray, Betray)를 선택하게 된다는 점이 이 문제의 ‘dilemma’이다.
Example (Cournot Duopoly)
기업1, 기업2의 생산량이 각각 \(q_1,q_2\)일 때, \(Q=q_1+q_2\), 시장의 수요 \(P(Q)=max\{a-Q,0\}\)Marginal Cost는 $c$이고, 두 기업은 동시에 생산량을 선택한다.
- \(N = \{1,2\}\) \(\quad\)
- \(S_i \in [0, \infty)\) \(\quad\)
- \(u_i(q_1,q_2)=(P(q_1+q_2)-c)q_i\) \(\quad\)
Definition (Pure Strategy)
\(S_i\)의 요소를 Pure Strategy라고 한다.
- Pure Strategy Nash Equilibrium (PSNE)
Definition (Mixed Strategy)
player $i$의 strategy space \(S_i\)의 요소들(=Pure Strategies)에 대한 probability distribution을 Mixed Strategy이라 한다.
Denoted by: \(\sigma_i \in \Delta(S_i)\)
- Finite \(S_i\)에 대해서는 \(\sigma_i : S_i \rightarrow [0,1] \quad s.t. \sum_{s_i \in S_i}\sigma_i(s_i)=1\) 이다.
- Uncountable \(S_i\)에 대해서는 sigma algebra의 개념이 필요
- Mixed Strategy Nash Equilibrium (MSNE)
Example (Matching Pennies)
가령 Player $A$가 H, T 두 개의 strategy를 모두 \(\frac{1}{2}\)의 확률로 수행한다면, \(\sigma_A(H)=\sigma_A(T)=\frac{1}{2}\) 이고, $\sigma_A = (\frac{1}{2}, \frac{1}{2})$ 와 같이 나타낼 수 있다.
Dominance, IDSDS
Definition (Dominance)
\[s_i' \in S_i \ \text{strictly dominates} \ s_i'' \in S_i \ \text{if} \ \forall s_{-i} \in S_{-i} \quad u(s_i', s_{-i}) > u(s_i'', s_{-i})\]Definition (Iterative Deletion of Strictly Dominated Strategies)
- Strictly dominated strategy를 반복적으로 계속해서 지운다.
- 다른 strategy를 strictly dominate하는 mixed strategy를 찾아내서 지울 수도 있다. strictly dominate하기만 하면 된다.
- 지우는 순서에 상관 없이 unique한 결과로 이어져야 한다.
- Weakly dominated strategy도 지우지 않는 이유는 unique한 결과로 이어지지 않을 수 있기 때문.
Nash Equilibrium
Definition
Strategy profile \(s^* = (s_i^*, s_{-i}^*) \in S\)는 다음의 조건을 만족시키면 Nash equilibrium이다.
\[s_i^* \in BR_i(s_{-i}^*)\]이때 BR(Best Response)의 정의는:
\[s_i \in S_i \ \text{is best response if} \ \forall s_i' \in S_i \quad u_i(s_i, \sigma_{-i}) \ge u_i(s_i', \sigma_{-i})\]이고, \(\sigma_{-i}\) 에 대한 Player $i$의 best response들의 집합을 \(BR_i(\sigma_{-i})\) 라고 한다.
Trembling Hand Perfect Equilibrium (THPE)
Motivation: dominated strategy가 포함된 N.E.는 제외하고 싶다
(자세한 내용 생략)
업데이트
2024.04.28
2024.06.21