Extensive Form Game, SPNE

Extensive Form Game

---

Motivation: 모든 player들이 동시에 선택을 하는 static game을 넘어서, player들이 sequential하게 선택하는 dynamics를 설계해보자.

Tree

트리 형태의 모델을 통해 위에서 아래의 순서로 player들이 선택을 하며 게임이 진행되는 과정을 표현할 수 있다.

Backward Induction

더 먼저 결정을 내려야 하는 player는 더 나중에 strategy를 선택하는 player를 고려하여 자신의 strategy를 선택한다.

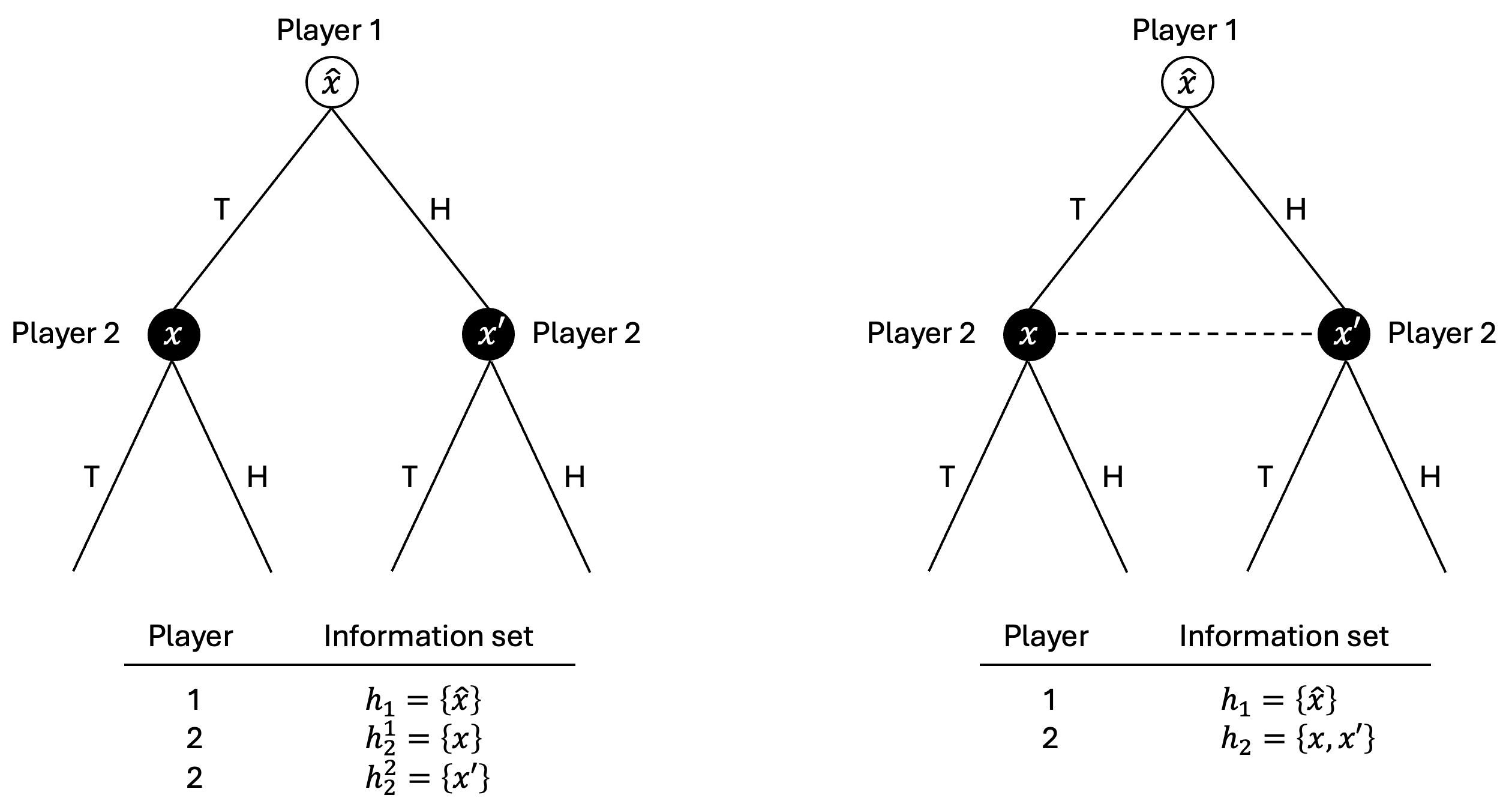
Information Set

• 노드들이 점선으로 연결되어 있는 경우는 non-singleton information set이라 하고, 해당 단계에서 player가 그 노드들 중 어떤 것이 현재 상황인지 알 수 없음을 뜻한다.

기타

• first mover가 항상 유리한 것은 아니다. (e.g. 가위바위보)

Definition (Subgame)

다음의 조건을 만족시킬 경우 extensive form game tree의 노드 $x$는 subgame의 루트가 된다.

노드 $x$ 또는 $x$의 자식 노드가, ($x$의 자식 노드가 아닌 노드를 포함하는 information set)에 포함되어서는 안된다.

• 루트 노드를 포함하지 않는 subgame은 proper subgame이라 한다.

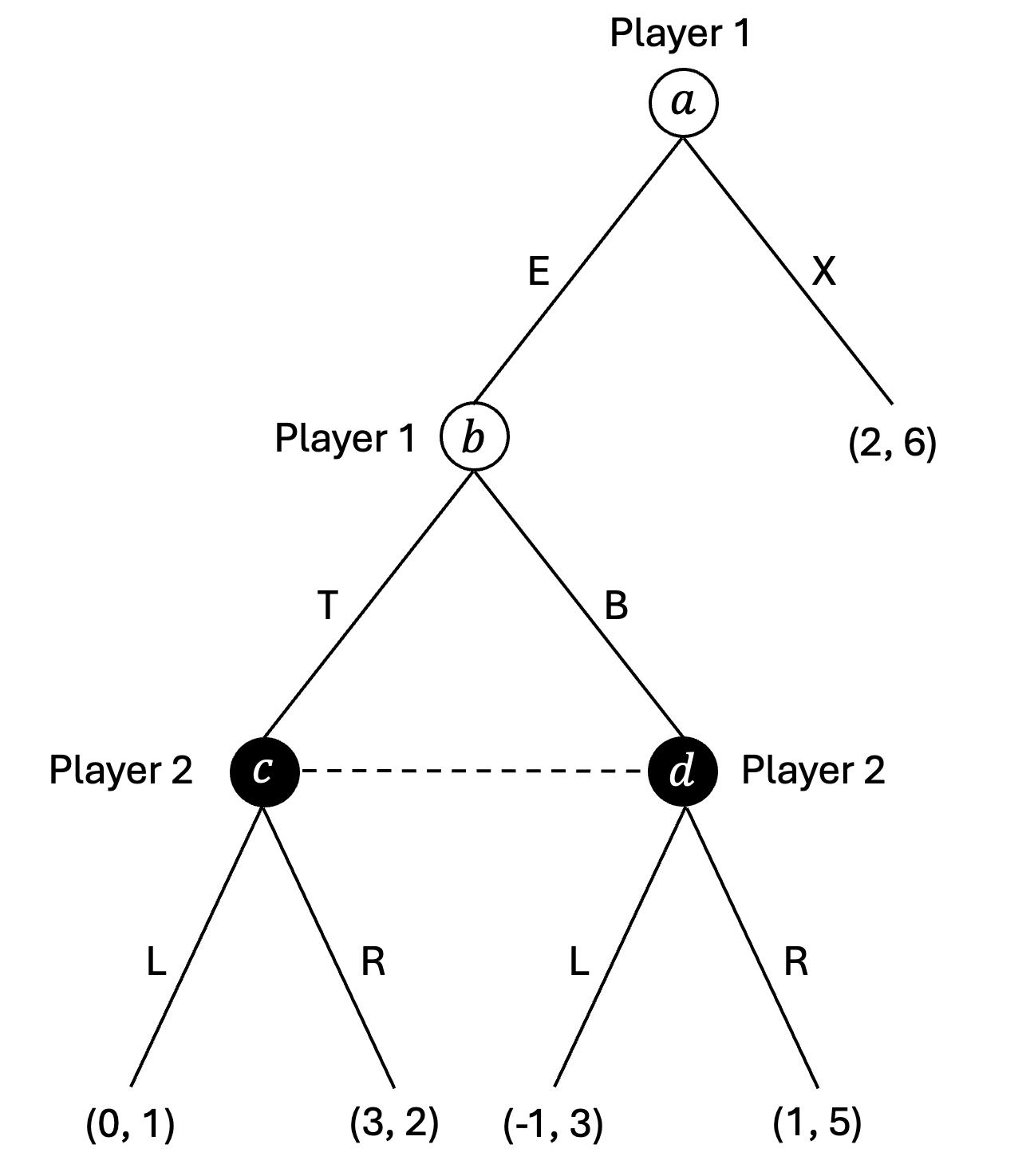
Example (Subgame)

• 가령 위의 extensive form game tree에서 $d$ 노드는 subgame의 루트 노드가 될 수 없다. $d$는 $d$의 자식 노드가 아닌 $c$ 노드를 포함하는 information set \(h=\{c,d\}\)에 포함되기 때문이다.
• 또한 위의 extensive form game tree에서 $b$ 노드는 subgame의 루트 노드가 될 수 있다.

Subgame Perfect Nash Equilibrium(SPNE)

Motivation: Backward Induction을 할 수 없는 경우*에 대한 해결책

* infinite horizon, imcomplete information 등

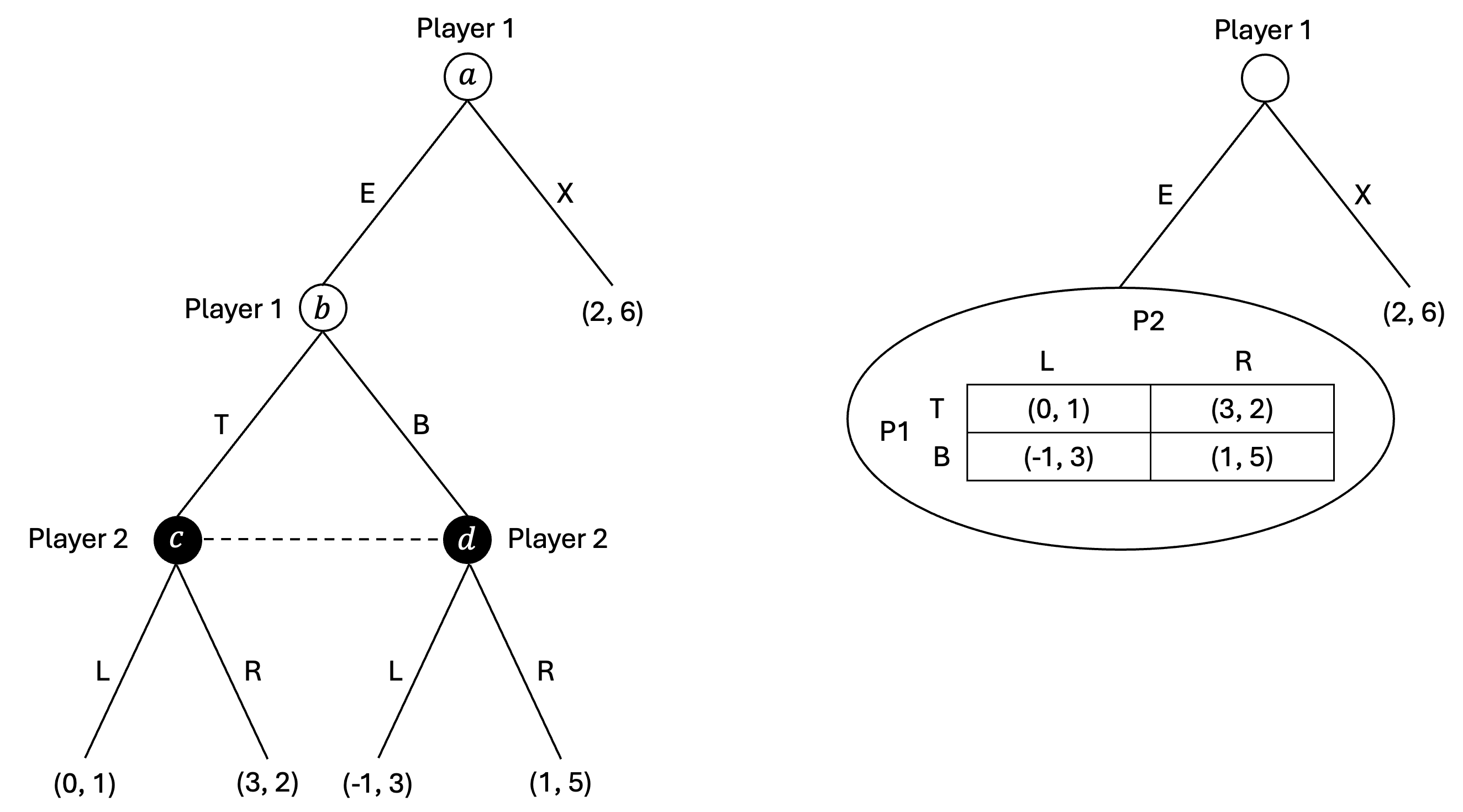
Example (SPNE)

1. 일단 전체 게임을 Normal Form으로 나타내서 Nash Equilibria를 모두 구하고
2. 그 다음 위와 같이 subgame을 찾아서 그 subgame에 대한 Nash Equilibria를 찾는다.
3. 전체 게임에 대한 N.E. 중 subgame에 대한 N.E.도 포함하는 것이 SPNE가 된다.

Forward Induction

SPNE들 중에서 convincing하지 않은 것을 제외할 때 사용됨. 자세한 내용은 생략

2024.06.22